- Skip to secondary menu
- Skip to main content
- Skip to primary sidebar
Statistics By Jim
Making statistics intuitive

Null Hypothesis: Definition, Rejecting & Examples
By Jim Frost 6 Comments
What is a Null Hypothesis?
The null hypothesis in statistics states that there is no difference between groups or no relationship between variables. It is one of two mutually exclusive hypotheses about a population in a hypothesis test.

- Null Hypothesis H 0 : No effect exists in the population.
- Alternative Hypothesis H A : The effect exists in the population.
In every study or experiment, researchers assess an effect or relationship. This effect can be the effectiveness of a new drug, building material, or other intervention that has benefits. There is a benefit or connection that the researchers hope to identify. Unfortunately, no effect may exist. In statistics, we call this lack of an effect the null hypothesis. Researchers assume that this notion of no effect is correct until they have enough evidence to suggest otherwise, similar to how a trial presumes innocence.
In this context, the analysts don’t necessarily believe the null hypothesis is correct. In fact, they typically want to reject it because that leads to more exciting finds about an effect or relationship. The new vaccine works!
You can think of it as the default theory that requires sufficiently strong evidence to reject. Like a prosecutor, researchers must collect sufficient evidence to overturn the presumption of no effect. Investigators must work hard to set up a study and a data collection system to obtain evidence that can reject the null hypothesis.
Related post : What is an Effect in Statistics?
Null Hypothesis Examples
Null hypotheses start as research questions that the investigator rephrases as a statement indicating there is no effect or relationship.
| Does the vaccine prevent infections? | The vaccine does not affect the infection rate. |
| Does the new additive increase product strength? | The additive does not affect mean product strength. |
| Does the exercise intervention increase bone mineral density? | The intervention does not affect bone mineral density. |
| As screen time increases, does test performance decrease? | There is no relationship between screen time and test performance. |
After reading these examples, you might think they’re a bit boring and pointless. However, the key is to remember that the null hypothesis defines the condition that the researchers need to discredit before suggesting an effect exists.
Let’s see how you reject the null hypothesis and get to those more exciting findings!
When to Reject the Null Hypothesis
So, you want to reject the null hypothesis, but how and when can you do that? To start, you’ll need to perform a statistical test on your data. The following is an overview of performing a study that uses a hypothesis test.
The first step is to devise a research question and the appropriate null hypothesis. After that, the investigators need to formulate an experimental design and data collection procedures that will allow them to gather data that can answer the research question. Then they collect the data. For more information about designing a scientific study that uses statistics, read my post 5 Steps for Conducting Studies with Statistics .
After data collection is complete, statistics and hypothesis testing enter the picture. Hypothesis testing takes your sample data and evaluates how consistent they are with the null hypothesis. The p-value is a crucial part of the statistical results because it quantifies how strongly the sample data contradict the null hypothesis.
When the sample data provide sufficient evidence, you can reject the null hypothesis. In a hypothesis test, this process involves comparing the p-value to your significance level .
Rejecting the Null Hypothesis
Reject the null hypothesis when the p-value is less than or equal to your significance level. Your sample data favor the alternative hypothesis, which suggests that the effect exists in the population. For a mnemonic device, remember—when the p-value is low, the null must go!
When you can reject the null hypothesis, your results are statistically significant. Learn more about Statistical Significance: Definition & Meaning .
Failing to Reject the Null Hypothesis
Conversely, when the p-value is greater than your significance level, you fail to reject the null hypothesis. The sample data provides insufficient data to conclude that the effect exists in the population. When the p-value is high, the null must fly!
Note that failing to reject the null is not the same as proving it. For more information about the difference, read my post about Failing to Reject the Null .
That’s a very general look at the process. But I hope you can see how the path to more exciting findings depends on being able to rule out the less exciting null hypothesis that states there’s nothing to see here!
Let’s move on to learning how to write the null hypothesis for different types of effects, relationships, and tests.
Related posts : How Hypothesis Tests Work and Interpreting P-values
How to Write a Null Hypothesis
The null hypothesis varies by the type of statistic and hypothesis test. Remember that inferential statistics use samples to draw conclusions about populations. Consequently, when you write a null hypothesis, it must make a claim about the relevant population parameter . Further, that claim usually indicates that the effect does not exist in the population. Below are typical examples of writing a null hypothesis for various parameters and hypothesis tests.
Related posts : Descriptive vs. Inferential Statistics and Populations, Parameters, and Samples in Inferential Statistics
Group Means
T-tests and ANOVA assess the differences between group means. For these tests, the null hypothesis states that there is no difference between group means in the population. In other words, the experimental conditions that define the groups do not affect the mean outcome. Mu (µ) is the population parameter for the mean, and you’ll need to include it in the statement for this type of study.
For example, an experiment compares the mean bone density changes for a new osteoporosis medication. The control group does not receive the medicine, while the treatment group does. The null states that the mean bone density changes for the control and treatment groups are equal.
- Null Hypothesis H 0 : Group means are equal in the population: µ 1 = µ 2 , or µ 1 – µ 2 = 0
- Alternative Hypothesis H A : Group means are not equal in the population: µ 1 ≠ µ 2 , or µ 1 – µ 2 ≠ 0.
Group Proportions
Proportions tests assess the differences between group proportions. For these tests, the null hypothesis states that there is no difference between group proportions. Again, the experimental conditions did not affect the proportion of events in the groups. P is the population proportion parameter that you’ll need to include.
For example, a vaccine experiment compares the infection rate in the treatment group to the control group. The treatment group receives the vaccine, while the control group does not. The null states that the infection rates for the control and treatment groups are equal.
- Null Hypothesis H 0 : Group proportions are equal in the population: p 1 = p 2 .
- Alternative Hypothesis H A : Group proportions are not equal in the population: p 1 ≠ p 2 .
Correlation and Regression Coefficients
Some studies assess the relationship between two continuous variables rather than differences between groups.
In these studies, analysts often use either correlation or regression analysis . For these tests, the null states that there is no relationship between the variables. Specifically, it says that the correlation or regression coefficient is zero. As one variable increases, there is no tendency for the other variable to increase or decrease. Rho (ρ) is the population correlation parameter and beta (β) is the regression coefficient parameter.
For example, a study assesses the relationship between screen time and test performance. The null states that there is no correlation between this pair of variables. As screen time increases, test performance does not tend to increase or decrease.
- Null Hypothesis H 0 : The correlation in the population is zero: ρ = 0.
- Alternative Hypothesis H A : The correlation in the population is not zero: ρ ≠ 0.
For all these cases, the analysts define the hypotheses before the study. After collecting the data, they perform a hypothesis test to determine whether they can reject the null hypothesis.
The preceding examples are all for two-tailed hypothesis tests. To learn about one-tailed tests and how to write a null hypothesis for them, read my post One-Tailed vs. Two-Tailed Tests .
Related post : Understanding Correlation
Neyman, J; Pearson, E. S. (January 1, 1933). On the Problem of the most Efficient Tests of Statistical Hypotheses . Philosophical Transactions of the Royal Society A . 231 (694–706): 289–337.
Share this:

Reader Interactions
January 11, 2024 at 2:57 pm
Thanks for the reply.
January 10, 2024 at 1:23 pm
Hi Jim, In your comment you state that equivalence test null and alternate hypotheses are reversed. For hypothesis tests of data fits to a probability distribution, the null hypothesis is that the probability distribution fits the data. Is this correct?
January 10, 2024 at 2:15 pm
Those two separate things, equivalence testing and normality tests. But, yes, you’re correct for both.
Hypotheses are switched for equivalence testing. You need to “work” (i.e., collect a large sample of good quality data) to be able to reject the null that the groups are different to be able to conclude they’re the same.
With typical hypothesis tests, if you have low quality data and a low sample size, you’ll fail to reject the null that they’re the same, concluding they’re equivalent. But that’s more a statement about the low quality and small sample size than anything to do with the groups being equal.
So, equivalence testing make you work to obtain a finding that the groups are the same (at least within some amount you define as a trivial difference).
For normality testing, and other distribution tests, the null states that the data follow the distribution (normal or whatever). If you reject the null, you have sufficient evidence to conclude that your sample data don’t follow the probability distribution. That’s a rare case where you hope to fail to reject the null. And it suffers from the problem I describe above where you might fail to reject the null simply because you have a small sample size. In that case, you’d conclude the data follow the probability distribution but it’s more that you don’t have enough data for the test to register the deviation. In this scenario, if you had a larger sample size, you’d reject the null and conclude it doesn’t follow that distribution.
I don’t know of any equivalence testing type approach for distribution fit tests where you’d need to work to show the data follow a distribution, although I haven’t looked for one either!
February 20, 2022 at 9:26 pm
Is a null hypothesis regularly (always) stated in the negative? “there is no” or “does not”
February 23, 2022 at 9:21 pm
Typically, the null hypothesis includes an equal sign. The null hypothesis states that the population parameter equals a particular value. That value is usually one that represents no effect. In the case of a one-sided hypothesis test, the null still contains an equal sign but it’s “greater than or equal to” or “less than or equal to.” If you wanted to translate the null hypothesis from its native mathematical expression, you could use the expression “there is no effect.” But the mathematical form more specifically states what it’s testing.
It’s the alternative hypothesis that typically contains does not equal.
There are some exceptions. For example, in an equivalence test where the researchers want to show that two things are equal, the null hypothesis states that they’re not equal.
In short, the null hypothesis states the condition that the researchers hope to reject. They need to work hard to set up an experiment and data collection that’ll gather enough evidence to be able to reject the null condition.
February 15, 2022 at 9:32 am
Dear sir I always read your notes on Research methods.. Kindly tell is there any available Book on all these..wonderfull Urgent
Comments and Questions Cancel reply
Have a language expert improve your writing
Run a free plagiarism check in 10 minutes, generate accurate citations for free.
- Knowledge Base
- Null and Alternative Hypotheses | Definitions & Examples
Null & Alternative Hypotheses | Definitions, Templates & Examples
Published on May 6, 2022 by Shaun Turney . Revised on June 22, 2023.
The null and alternative hypotheses are two competing claims that researchers weigh evidence for and against using a statistical test :
- Null hypothesis ( H 0 ): There’s no effect in the population .
- Alternative hypothesis ( H a or H 1 ) : There’s an effect in the population.
Table of contents
Answering your research question with hypotheses, what is a null hypothesis, what is an alternative hypothesis, similarities and differences between null and alternative hypotheses, how to write null and alternative hypotheses, other interesting articles, frequently asked questions.
The null and alternative hypotheses offer competing answers to your research question . When the research question asks “Does the independent variable affect the dependent variable?”:
- The null hypothesis ( H 0 ) answers “No, there’s no effect in the population.”
- The alternative hypothesis ( H a ) answers “Yes, there is an effect in the population.”
The null and alternative are always claims about the population. That’s because the goal of hypothesis testing is to make inferences about a population based on a sample . Often, we infer whether there’s an effect in the population by looking at differences between groups or relationships between variables in the sample. It’s critical for your research to write strong hypotheses .
You can use a statistical test to decide whether the evidence favors the null or alternative hypothesis. Each type of statistical test comes with a specific way of phrasing the null and alternative hypothesis. However, the hypotheses can also be phrased in a general way that applies to any test.
Receive feedback on language, structure, and formatting
Professional editors proofread and edit your paper by focusing on:
- Academic style
- Vague sentences
- Style consistency
See an example

The null hypothesis is the claim that there’s no effect in the population.
If the sample provides enough evidence against the claim that there’s no effect in the population ( p ≤ α), then we can reject the null hypothesis . Otherwise, we fail to reject the null hypothesis.
Although “fail to reject” may sound awkward, it’s the only wording that statisticians accept . Be careful not to say you “prove” or “accept” the null hypothesis.
Null hypotheses often include phrases such as “no effect,” “no difference,” or “no relationship.” When written in mathematical terms, they always include an equality (usually =, but sometimes ≥ or ≤).
You can never know with complete certainty whether there is an effect in the population. Some percentage of the time, your inference about the population will be incorrect. When you incorrectly reject the null hypothesis, it’s called a type I error . When you incorrectly fail to reject it, it’s a type II error.
Examples of null hypotheses
The table below gives examples of research questions and null hypotheses. There’s always more than one way to answer a research question, but these null hypotheses can help you get started.
| ( ) | ||
| Does tooth flossing affect the number of cavities? | Tooth flossing has on the number of cavities. | test: The mean number of cavities per person does not differ between the flossing group (µ ) and the non-flossing group (µ ) in the population; µ = µ . |
| Does the amount of text highlighted in the textbook affect exam scores? | The amount of text highlighted in the textbook has on exam scores. | : There is no relationship between the amount of text highlighted and exam scores in the population; β = 0. |
| Does daily meditation decrease the incidence of depression? | Daily meditation the incidence of depression.* | test: The proportion of people with depression in the daily-meditation group ( ) is greater than or equal to the no-meditation group ( ) in the population; ≥ . |
*Note that some researchers prefer to always write the null hypothesis in terms of “no effect” and “=”. It would be fine to say that daily meditation has no effect on the incidence of depression and p 1 = p 2 .
The alternative hypothesis ( H a ) is the other answer to your research question . It claims that there’s an effect in the population.
Often, your alternative hypothesis is the same as your research hypothesis. In other words, it’s the claim that you expect or hope will be true.
The alternative hypothesis is the complement to the null hypothesis. Null and alternative hypotheses are exhaustive, meaning that together they cover every possible outcome. They are also mutually exclusive, meaning that only one can be true at a time.
Alternative hypotheses often include phrases such as “an effect,” “a difference,” or “a relationship.” When alternative hypotheses are written in mathematical terms, they always include an inequality (usually ≠, but sometimes < or >). As with null hypotheses, there are many acceptable ways to phrase an alternative hypothesis.
Examples of alternative hypotheses
The table below gives examples of research questions and alternative hypotheses to help you get started with formulating your own.
| Does tooth flossing affect the number of cavities? | Tooth flossing has an on the number of cavities. | test: The mean number of cavities per person differs between the flossing group (µ ) and the non-flossing group (µ ) in the population; µ ≠ µ . |
| Does the amount of text highlighted in a textbook affect exam scores? | The amount of text highlighted in the textbook has an on exam scores. | : There is a relationship between the amount of text highlighted and exam scores in the population; β ≠ 0. |
| Does daily meditation decrease the incidence of depression? | Daily meditation the incidence of depression. | test: The proportion of people with depression in the daily-meditation group ( ) is less than the no-meditation group ( ) in the population; < . |
Null and alternative hypotheses are similar in some ways:
- They’re both answers to the research question.
- They both make claims about the population.
- They’re both evaluated by statistical tests.
However, there are important differences between the two types of hypotheses, summarized in the following table.
| A claim that there is in the population. | A claim that there is in the population. | |
|
| ||
| Equality symbol (=, ≥, or ≤) | Inequality symbol (≠, <, or >) | |
| Rejected | Supported | |
| Failed to reject | Not supported |
To help you write your hypotheses, you can use the template sentences below. If you know which statistical test you’re going to use, you can use the test-specific template sentences. Otherwise, you can use the general template sentences.
General template sentences
The only thing you need to know to use these general template sentences are your dependent and independent variables. To write your research question, null hypothesis, and alternative hypothesis, fill in the following sentences with your variables:
Does independent variable affect dependent variable ?
- Null hypothesis ( H 0 ): Independent variable does not affect dependent variable.
- Alternative hypothesis ( H a ): Independent variable affects dependent variable.
Test-specific template sentences
Once you know the statistical test you’ll be using, you can write your hypotheses in a more precise and mathematical way specific to the test you chose. The table below provides template sentences for common statistical tests.
| ( ) | ||
| test
with two groups | The mean dependent variable does not differ between group 1 (µ ) and group 2 (µ ) in the population; µ = µ . | The mean dependent variable differs between group 1 (µ ) and group 2 (µ ) in the population; µ ≠ µ . |
| with three groups | The mean dependent variable does not differ between group 1 (µ ), group 2 (µ ), and group 3 (µ ) in the population; µ = µ = µ . | The mean dependent variable of group 1 (µ ), group 2 (µ ), and group 3 (µ ) are not all equal in the population. |
| There is no correlation between independent variable and dependent variable in the population; ρ = 0. | There is a correlation between independent variable and dependent variable in the population; ρ ≠ 0. | |
| There is no relationship between independent variable and dependent variable in the population; β = 0. | There is a relationship between independent variable and dependent variable in the population; β ≠ 0. | |
| Two-proportions test | The dependent variable expressed as a proportion does not differ between group 1 ( ) and group 2 ( ) in the population; = . | The dependent variable expressed as a proportion differs between group 1 ( ) and group 2 ( ) in the population; ≠ . |
Note: The template sentences above assume that you’re performing one-tailed tests . One-tailed tests are appropriate for most studies.
If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.
- Normal distribution
- Descriptive statistics
- Measures of central tendency
- Correlation coefficient
Methodology
- Cluster sampling
- Stratified sampling
- Types of interviews
- Cohort study
- Thematic analysis
Research bias
- Implicit bias
- Cognitive bias
- Survivorship bias
- Availability heuristic
- Nonresponse bias
- Regression to the mean
Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.
Null and alternative hypotheses are used in statistical hypothesis testing . The null hypothesis of a test always predicts no effect or no relationship between variables, while the alternative hypothesis states your research prediction of an effect or relationship.
The null hypothesis is often abbreviated as H 0 . When the null hypothesis is written using mathematical symbols, it always includes an equality symbol (usually =, but sometimes ≥ or ≤).
The alternative hypothesis is often abbreviated as H a or H 1 . When the alternative hypothesis is written using mathematical symbols, it always includes an inequality symbol (usually ≠, but sometimes < or >).
A research hypothesis is your proposed answer to your research question. The research hypothesis usually includes an explanation (“ x affects y because …”).
A statistical hypothesis, on the other hand, is a mathematical statement about a population parameter. Statistical hypotheses always come in pairs: the null and alternative hypotheses . In a well-designed study , the statistical hypotheses correspond logically to the research hypothesis.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
Turney, S. (2023, June 22). Null & Alternative Hypotheses | Definitions, Templates & Examples. Scribbr. Retrieved August 12, 2024, from https://www.scribbr.com/statistics/null-and-alternative-hypotheses/
Is this article helpful?

Shaun Turney
Other students also liked, inferential statistics | an easy introduction & examples, hypothesis testing | a step-by-step guide with easy examples, type i & type ii errors | differences, examples, visualizations, what is your plagiarism score.
What is The Null Hypothesis & When Do You Reject The Null Hypothesis
Julia Simkus
Editor at Simply Psychology
BA (Hons) Psychology, Princeton University
Julia Simkus is a graduate of Princeton University with a Bachelor of Arts in Psychology. She is currently studying for a Master's Degree in Counseling for Mental Health and Wellness in September 2023. Julia's research has been published in peer reviewed journals.
Learn about our Editorial Process
Saul McLeod, PhD
Editor-in-Chief for Simply Psychology
BSc (Hons) Psychology, MRes, PhD, University of Manchester
Saul McLeod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.
Olivia Guy-Evans, MSc
Associate Editor for Simply Psychology
BSc (Hons) Psychology, MSc Psychology of Education
Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.
On This Page:
A null hypothesis is a statistical concept suggesting no significant difference or relationship between measured variables. It’s the default assumption unless empirical evidence proves otherwise.
The null hypothesis states no relationship exists between the two variables being studied (i.e., one variable does not affect the other).
The null hypothesis is the statement that a researcher or an investigator wants to disprove.
Testing the null hypothesis can tell you whether your results are due to the effects of manipulating the dependent variable or due to random chance.
How to Write a Null Hypothesis
Null hypotheses (H0) start as research questions that the investigator rephrases as statements indicating no effect or relationship between the independent and dependent variables.
It is a default position that your research aims to challenge or confirm.
For example, if studying the impact of exercise on weight loss, your null hypothesis might be:
There is no significant difference in weight loss between individuals who exercise daily and those who do not.
Examples of Null Hypotheses
| Research Question | Null Hypothesis |
|---|---|
| Do teenagers use cell phones more than adults? | Teenagers and adults use cell phones the same amount. |
| Do tomato plants exhibit a higher rate of growth when planted in compost rather than in soil? | Tomato plants show no difference in growth rates when planted in compost rather than soil. |
| Does daily meditation decrease the incidence of depression? | Daily meditation does not decrease the incidence of depression. |
| Does daily exercise increase test performance? | There is no relationship between daily exercise time and test performance. |
| Does the new vaccine prevent infections? | The vaccine does not affect the infection rate. |
| Does flossing your teeth affect the number of cavities? | Flossing your teeth has no effect on the number of cavities. |
When Do We Reject The Null Hypothesis?
We reject the null hypothesis when the data provide strong enough evidence to conclude that it is likely incorrect. This often occurs when the p-value (probability of observing the data given the null hypothesis is true) is below a predetermined significance level.
If the collected data does not meet the expectation of the null hypothesis, a researcher can conclude that the data lacks sufficient evidence to back up the null hypothesis, and thus the null hypothesis is rejected.
Rejecting the null hypothesis means that a relationship does exist between a set of variables and the effect is statistically significant ( p > 0.05).
If the data collected from the random sample is not statistically significance , then the null hypothesis will be accepted, and the researchers can conclude that there is no relationship between the variables.
You need to perform a statistical test on your data in order to evaluate how consistent it is with the null hypothesis. A p-value is one statistical measurement used to validate a hypothesis against observed data.
Calculating the p-value is a critical part of null-hypothesis significance testing because it quantifies how strongly the sample data contradicts the null hypothesis.
The level of statistical significance is often expressed as a p -value between 0 and 1. The smaller the p-value, the stronger the evidence that you should reject the null hypothesis.

Usually, a researcher uses a confidence level of 95% or 99% (p-value of 0.05 or 0.01) as general guidelines to decide if you should reject or keep the null.
When your p-value is less than or equal to your significance level, you reject the null hypothesis.
In other words, smaller p-values are taken as stronger evidence against the null hypothesis. Conversely, when the p-value is greater than your significance level, you fail to reject the null hypothesis.
In this case, the sample data provides insufficient data to conclude that the effect exists in the population.
Because you can never know with complete certainty whether there is an effect in the population, your inferences about a population will sometimes be incorrect.
When you incorrectly reject the null hypothesis, it’s called a type I error. When you incorrectly fail to reject it, it’s called a type II error.
Why Do We Never Accept The Null Hypothesis?
The reason we do not say “accept the null” is because we are always assuming the null hypothesis is true and then conducting a study to see if there is evidence against it. And, even if we don’t find evidence against it, a null hypothesis is not accepted.
A lack of evidence only means that you haven’t proven that something exists. It does not prove that something doesn’t exist.
It is risky to conclude that the null hypothesis is true merely because we did not find evidence to reject it. It is always possible that researchers elsewhere have disproved the null hypothesis, so we cannot accept it as true, but instead, we state that we failed to reject the null.
One can either reject the null hypothesis, or fail to reject it, but can never accept it.
Why Do We Use The Null Hypothesis?
We can never prove with 100% certainty that a hypothesis is true; We can only collect evidence that supports a theory. However, testing a hypothesis can set the stage for rejecting or accepting this hypothesis within a certain confidence level.
The null hypothesis is useful because it can tell us whether the results of our study are due to random chance or the manipulation of a variable (with a certain level of confidence).
A null hypothesis is rejected if the measured data is significantly unlikely to have occurred and a null hypothesis is accepted if the observed outcome is consistent with the position held by the null hypothesis.
Rejecting the null hypothesis sets the stage for further experimentation to see if a relationship between two variables exists.
Hypothesis testing is a critical part of the scientific method as it helps decide whether the results of a research study support a particular theory about a given population. Hypothesis testing is a systematic way of backing up researchers’ predictions with statistical analysis.
It helps provide sufficient statistical evidence that either favors or rejects a certain hypothesis about the population parameter.
Purpose of a Null Hypothesis
- The primary purpose of the null hypothesis is to disprove an assumption.
- Whether rejected or accepted, the null hypothesis can help further progress a theory in many scientific cases.
- A null hypothesis can be used to ascertain how consistent the outcomes of multiple studies are.
Do you always need both a Null Hypothesis and an Alternative Hypothesis?
The null (H0) and alternative (Ha or H1) hypotheses are two competing claims that describe the effect of the independent variable on the dependent variable. They are mutually exclusive, which means that only one of the two hypotheses can be true.
While the null hypothesis states that there is no effect in the population, an alternative hypothesis states that there is statistical significance between two variables.
The goal of hypothesis testing is to make inferences about a population based on a sample. In order to undertake hypothesis testing, you must express your research hypothesis as a null and alternative hypothesis. Both hypotheses are required to cover every possible outcome of the study.
What is the difference between a null hypothesis and an alternative hypothesis?
The alternative hypothesis is the complement to the null hypothesis. The null hypothesis states that there is no effect or no relationship between variables, while the alternative hypothesis claims that there is an effect or relationship in the population.
It is the claim that you expect or hope will be true. The null hypothesis and the alternative hypothesis are always mutually exclusive, meaning that only one can be true at a time.
What are some problems with the null hypothesis?
One major problem with the null hypothesis is that researchers typically will assume that accepting the null is a failure of the experiment. However, accepting or rejecting any hypothesis is a positive result. Even if the null is not refuted, the researchers will still learn something new.
Why can a null hypothesis not be accepted?
We can either reject or fail to reject a null hypothesis, but never accept it. If your test fails to detect an effect, this is not proof that the effect doesn’t exist. It just means that your sample did not have enough evidence to conclude that it exists.
We can’t accept a null hypothesis because a lack of evidence does not prove something that does not exist. Instead, we fail to reject it.
Failing to reject the null indicates that the sample did not provide sufficient enough evidence to conclude that an effect exists.
If the p-value is greater than the significance level, then you fail to reject the null hypothesis.
Is a null hypothesis directional or non-directional?
A hypothesis test can either contain an alternative directional hypothesis or a non-directional alternative hypothesis. A directional hypothesis is one that contains the less than (“<“) or greater than (“>”) sign.
A nondirectional hypothesis contains the not equal sign (“≠”). However, a null hypothesis is neither directional nor non-directional.
A null hypothesis is a prediction that there will be no change, relationship, or difference between two variables.
The directional hypothesis or nondirectional hypothesis would then be considered alternative hypotheses to the null hypothesis.
Gill, J. (1999). The insignificance of null hypothesis significance testing. Political research quarterly , 52 (3), 647-674.
Krueger, J. (2001). Null hypothesis significance testing: On the survival of a flawed method. American Psychologist , 56 (1), 16.
Masson, M. E. (2011). A tutorial on a practical Bayesian alternative to null-hypothesis significance testing. Behavior research methods , 43 , 679-690.
Nickerson, R. S. (2000). Null hypothesis significance testing: a review of an old and continuing controversy. Psychological methods , 5 (2), 241.
Rozeboom, W. W. (1960). The fallacy of the null-hypothesis significance test. Psychological bulletin , 57 (5), 416.
9.1 Null and Alternative Hypotheses
The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.
H 0 , the — null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.
H a —, the alternative hypothesis: a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .
Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.
After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are reject H 0 if the sample information favors the alternative hypothesis or do not reject H 0 or decline to reject H 0 if the sample information is insufficient to reject the null hypothesis.
Mathematical Symbols Used in H 0 and H a :
| equal (=) | not equal (≠) greater than (>) less than (<) |
| greater than or equal to (≥) | less than (<) |
| less than or equal to (≤) | more than (>) |
H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.
Example 9.1
H 0 : No more than 30 percent of the registered voters in Santa Clara County voted in the primary election. p ≤ 30 H a : More than 30 percent of the registered voters in Santa Clara County voted in the primary election. p > 30
A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25 percent. State the null and alternative hypotheses.
Example 9.2
We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are the following: H 0 : μ = 2.0 H a : μ ≠ 2.0
We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : μ __ 66
- H a : μ __ 66
Example 9.3
We want to test if college students take fewer than five years to graduate from college, on the average. The null and alternative hypotheses are the following: H 0 : μ ≥ 5 H a : μ < 5
We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : μ __ 45
- H a : μ __ 45
Example 9.4
An article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third of the students pass. The same article stated that 6.6 percent of U.S. students take advanced placement exams and 4.4 percent pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6 percent. State the null and alternative hypotheses. H 0 : p ≤ 0.066 H a : p > 0.066
On a state driver’s test, about 40 percent pass the test on the first try. We want to test if more than 40 percent pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : p __ 0.40
- H a : p __ 0.40
Collaborative Exercise
Bring to class a newspaper, some news magazines, and some internet articles. In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-statistics . Changes were made to the original material, including updates to art, structure, and other content updates.
Access for free at https://openstax.org/books/statistics/pages/1-introduction
- Authors: Barbara Illowsky, Susan Dean
- Publisher/website: OpenStax
- Book title: Statistics
- Publication date: Mar 27, 2020
- Location: Houston, Texas
- Book URL: https://openstax.org/books/statistics/pages/1-introduction
- Section URL: https://openstax.org/books/statistics/pages/9-1-null-and-alternative-hypotheses
© Apr 16, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
AP®︎/College Statistics
Course: ap®︎/college statistics > unit 10.
- Idea behind hypothesis testing
Examples of null and alternative hypotheses
- Writing null and alternative hypotheses
- P-values and significance tests
- Comparing P-values to different significance levels
- Estimating a P-value from a simulation
- Estimating P-values from simulations
- Using P-values to make conclusions
Want to join the conversation?
- Upvote Button navigates to signup page
- Downvote Button navigates to signup page
- Flag Button navigates to signup page

Video transcript
User Preferences
Content preview.
Arcu felis bibendum ut tristique et egestas quis:
- Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
- Duis aute irure dolor in reprehenderit in voluptate
- Excepteur sint occaecat cupidatat non proident
Keyboard Shortcuts
10.1 - setting the hypotheses: examples.
A significance test examines whether the null hypothesis provides a plausible explanation of the data. The null hypothesis itself does not involve the data. It is a statement about a parameter (a numerical characteristic of the population). These population values might be proportions or means or differences between means or proportions or correlations or odds ratios or any other numerical summary of the population. The alternative hypothesis is typically the research hypothesis of interest. Here are some examples.
Example 10.2: Hypotheses with One Sample of One Categorical Variable Section
About 10% of the human population is left-handed. Suppose a researcher at Penn State speculates that students in the College of Arts and Architecture are more likely to be left-handed than people found in the general population. We only have one sample since we will be comparing a population proportion based on a sample value to a known population value.
- Research Question : Are artists more likely to be left-handed than people found in the general population?
- Response Variable : Classification of the student as either right-handed or left-handed
State Null and Alternative Hypotheses
- Null Hypothesis : Students in the College of Arts and Architecture are no more likely to be left-handed than people in the general population (population percent of left-handed students in the College of Art and Architecture = 10% or p = .10).
- Alternative Hypothesis : Students in the College of Arts and Architecture are more likely to be left-handed than people in the general population (population percent of left-handed students in the College of Arts and Architecture > 10% or p > .10). This is a one-sided alternative hypothesis.
Example 10.3: Hypotheses with One Sample of One Measurement Variable Section

A generic brand of the anti-histamine Diphenhydramine markets a capsule with a 50 milligram dose. The manufacturer is worried that the machine that fills the capsules has come out of calibration and is no longer creating capsules with the appropriate dosage.
- Research Question : Does the data suggest that the population mean dosage of this brand is different than 50 mg?
- Response Variable : dosage of the active ingredient found by a chemical assay.
- Null Hypothesis : On the average, the dosage sold under this brand is 50 mg (population mean dosage = 50 mg).
- Alternative Hypothesis : On the average, the dosage sold under this brand is not 50 mg (population mean dosage ≠ 50 mg). This is a two-sided alternative hypothesis.
Example 10.4: Hypotheses with Two Samples of One Categorical Variable Section

Many people are starting to prefer vegetarian meals on a regular basis. Specifically, a researcher believes that females are more likely than males to eat vegetarian meals on a regular basis.
- Research Question : Does the data suggest that females are more likely than males to eat vegetarian meals on a regular basis?
- Response Variable : Classification of whether or not a person eats vegetarian meals on a regular basis
- Explanatory (Grouping) Variable: Sex
- Null Hypothesis : There is no sex effect regarding those who eat vegetarian meals on a regular basis (population percent of females who eat vegetarian meals on a regular basis = population percent of males who eat vegetarian meals on a regular basis or p females = p males ).
- Alternative Hypothesis : Females are more likely than males to eat vegetarian meals on a regular basis (population percent of females who eat vegetarian meals on a regular basis > population percent of males who eat vegetarian meals on a regular basis or p females > p males ). This is a one-sided alternative hypothesis.
Example 10.5: Hypotheses with Two Samples of One Measurement Variable Section

Obesity is a major health problem today. Research is starting to show that people may be able to lose more weight on a low carbohydrate diet than on a low fat diet.
- Research Question : Does the data suggest that, on the average, people are able to lose more weight on a low carbohydrate diet than on a low fat diet?
- Response Variable : Weight loss (pounds)
- Explanatory (Grouping) Variable : Type of diet
- Null Hypothesis : There is no difference in the mean amount of weight loss when comparing a low carbohydrate diet with a low fat diet (population mean weight loss on a low carbohydrate diet = population mean weight loss on a low fat diet).
- Alternative Hypothesis : The mean weight loss should be greater for those on a low carbohydrate diet when compared with those on a low fat diet (population mean weight loss on a low carbohydrate diet > population mean weight loss on a low fat diet). This is a one-sided alternative hypothesis.
Example 10.6: Hypotheses about the relationship between Two Categorical Variables Section
- Research Question : Do the odds of having a stroke increase if you inhale second hand smoke ? A case-control study of non-smoking stroke patients and controls of the same age and occupation are asked if someone in their household smokes.
- Variables : There are two different categorical variables (Stroke patient vs control and whether the subject lives in the same household as a smoker). Living with a smoker (or not) is the natural explanatory variable and having a stroke (or not) is the natural response variable in this situation.
- Null Hypothesis : There is no relationship between whether or not a person has a stroke and whether or not a person lives with a smoker (odds ratio between stroke and second-hand smoke situation is = 1).
- Alternative Hypothesis : There is a relationship between whether or not a person has a stroke and whether or not a person lives with a smoker (odds ratio between stroke and second-hand smoke situation is > 1). This is a one-tailed alternative.
This research question might also be addressed like example 11.4 by making the hypotheses about comparing the proportion of stroke patients that live with smokers to the proportion of controls that live with smokers.
Example 10.7: Hypotheses about the relationship between Two Measurement Variables Section
- Research Question : A financial analyst believes there might be a positive association between the change in a stock's price and the amount of the stock purchased by non-management employees the previous day (stock trading by management being under "insider-trading" regulatory restrictions).
- Variables : Daily price change information (the response variable) and previous day stock purchases by non-management employees (explanatory variable). These are two different measurement variables.
- Null Hypothesis : The correlation between the daily stock price change (\$) and the daily stock purchases by non-management employees (\$) = 0.
- Alternative Hypothesis : The correlation between the daily stock price change (\$) and the daily stock purchases by non-management employees (\$) > 0. This is a one-sided alternative hypothesis.
Example 10.8: Hypotheses about comparing the relationship between Two Measurement Variables in Two Samples Section
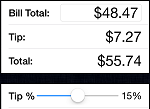
- Research Question : Is there a linear relationship between the amount of the bill (\$) at a restaurant and the tip (\$) that was left. Is the strength of this association different for family restaurants than for fine dining restaurants?
- Variables : There are two different measurement variables. The size of the tip would depend on the size of the bill so the amount of the bill would be the explanatory variable and the size of the tip would be the response variable.
- Null Hypothesis : The correlation between the amount of the bill (\$) at a restaurant and the tip (\$) that was left is the same at family restaurants as it is at fine dining restaurants.
- Alternative Hypothesis : The correlation between the amount of the bill (\$) at a restaurant and the tip (\$) that was left is the difference at family restaurants then it is at fine dining restaurants. This is a two-sided alternative hypothesis.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
Chapter 13: Inferential Statistics
Some Basic Null Hypothesis Tests
Learning Objectives
- Conduct and interpret one-sample, dependent-samples, and independent-samples t tests.
- Interpret the results of one-way, repeated measures, and factorial ANOVAs.
- Conduct and interpret null hypothesis tests of Pearson’s r .
In this section, we look at several common null hypothesis testing procedures. The emphasis here is on providing enough information to allow you to conduct and interpret the most basic versions. In most cases, the online statistical analysis tools mentioned in Chapter 12 will handle the computations—as will programs such as Microsoft Excel and SPSS.
The t Test
As we have seen throughout this book, many studies in psychology focus on the difference between two means. The most common null hypothesis test for this type of statistical relationship is the t test . In this section, we look at three types of t tests that are used for slightly different research designs: the one-sample t test, the dependent-samples t test, and the independent-samples t test.
One-Sample t Test
The one-sample t test is used to compare a sample mean ( M ) with a hypothetical population mean (μ0) that provides some interesting standard of comparison. The null hypothesis is that the mean for the population (µ) is equal to the hypothetical population mean: μ = μ0. The alternative hypothesis is that the mean for the population is different from the hypothetical population mean: μ ≠ μ0. To decide between these two hypotheses, we need to find the probability of obtaining the sample mean (or one more extreme) if the null hypothesis were true. But finding this p value requires first computing a test statistic called t . (A test statistic is a statistic that is computed only to help find the p value.) The formula for t is as follows:
![Rendered by QuickLaTeX.com \[t=\dfrac{M-\mu_0}{\left(\dfrac{SD}{\sqrt{N}}\right)}\]](https://opentextbc.ca/researchmethods/wp-content/ql-cache/quicklatex.com-5cabf5ed8125558a7361164aadc41c78_l3.png)
Again, M is the sample mean and µ 0 is the hypothetical population mean of interest. SD is the sample standard deviation and N is the sample size.
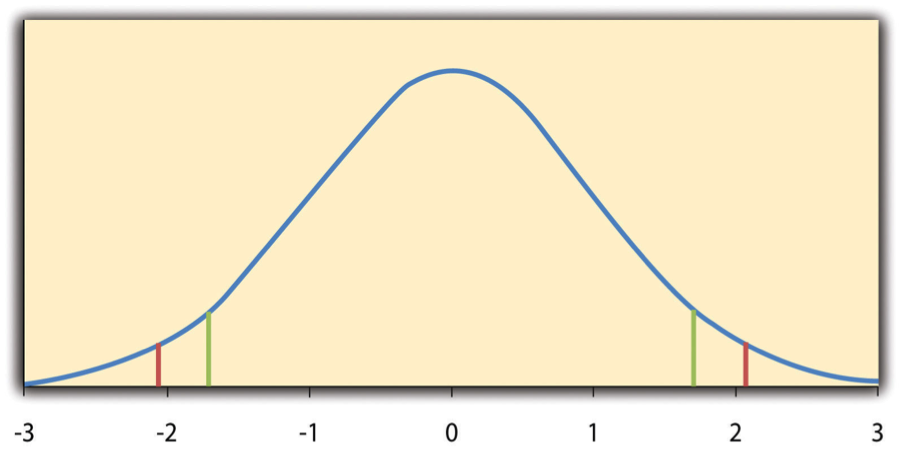
The reason the t statistic (or any test statistic) is useful is that we know how it is distributed when the null hypothesis is true. As shown in Figure 13.1, this distribution is unimodal and symmetrical, and it has a mean of 0. Its precise shape depends on a statistical concept called the degrees of freedom, which for a one-sample t test is N − 1. (There are 24 degrees of freedom for the distribution shown in Figure 13.1.) The important point is that knowing this distribution makes it possible to find the p value for any t score. Consider, for example, a t score of +1.50 based on a sample of 25. The probability of a t score at least this extreme is given by the proportion of t scores in the distribution that are at least this extreme. For now, let us define extreme as being far from zero in either direction. Thus the p value is the proportion of t scores that are +1.50 or above or that are −1.50 or below—a value that turns out to be .14.
Fortunately, we do not have to deal directly with the distribution of t scores. If we were to enter our sample data and hypothetical mean of interest into one of the online statistical tools in Chapter 12 or into a program like SPSS (Excel does not have a one-sample t test function), the output would include both the t score and the p value. At this point, the rest of the procedure is simple. If p is less than .05, we reject the null hypothesis and conclude that the population mean differs from the hypothetical mean of interest. If p is greater than .05, we retain the null hypothesis and conclude that there is not enough evidence to say that the population mean differs from the hypothetical mean of interest. (Again, technically, we conclude only that we do not have enough evidence to conclude that it does differ.)
If we were to compute the t score by hand, we could use a table like Table 13.2 to make the decision. This table does not provide actual p values. Instead, it provides the critical values of t for different degrees of freedom ( df) when α is .05. For now, let us focus on the two-tailed critical values in the last column of the table. Each of these values should be interpreted as a pair of values: one positive and one negative. For example, the two-tailed critical values when there are 24 degrees of freedom are +2.064 and −2.064. These are represented by the red vertical lines in Figure 13.1. The idea is that any t score below the lower critical value (the left-hand red line in Figure 13.1) is in the lowest 2.5% of the distribution, while any t score above the upper critical value (the right-hand red line) is in the highest 2.5% of the distribution. Therefore any t score beyond the critical value in either direction is in the most extreme 5% of t scores when the null hypothesis is true and has a p value less than .05. Thus if the t score we compute is beyond the critical value in either direction, then we reject the null hypothesis. If the t score we compute is between the upper and lower critical values, then we retain the null hypothesis.
| One-tailed critical value | Two-tailed critical value | |
|---|---|---|
| 3 | 2.353 | 3.182 |
| 4 | 2.132 | 2.776 |
| 5 | 2.015 | 2.571 |
| 6 | 1.943 | 2.447 |
| 7 | 1.895 | 2.365 |
| 8 | 1.860 | 2.306 |
| 9 | 1.833 | 2.262 |
| 10 | 1.812 | 2.228 |
| 11 | 1.796 | 2.201 |
| 12 | 1.782 | 2.179 |
| 13 | 1.771 | 2.160 |
| 14 | 1.761 | 2.145 |
| 15 | 1.753 | 2.131 |
| 16 | 1.746 | 2.120 |
| 17 | 1.740 | 2.110 |
| 18 | 1.734 | 2.101 |
| 19 | 1.729 | 2.093 |
| 20 | 1.725 | 2.086 |
| 21 | 1.721 | 2.080 |
| 22 | 1.717 | 2.074 |
| 23 | 1.714 | 2.069 |
| 24 | 1.711 | 2.064 |
| 25 | 1.708 | 2.060 |
| 30 | 1.697 | 2.042 |
| 35 | 1.690 | 2.030 |
| 40 | 1.684 | 2.021 |
| 45 | 1.679 | 2.014 |
| 50 | 1.676 | 2.009 |
| 60 | 1.671 | 2.000 |
| 70 | 1.667 | 1.994 |
| 80 | 1.664 | 1.990 |
| 90 | 1.662 | 1.987 |
| 100 | 1.660 | 1.984 |
Thus far, we have considered what is called a two-tailed test , where we reject the null hypothesis if the t score for the sample is extreme in either direction. This test makes sense when we believe that the sample mean might differ from the hypothetical population mean but we do not have good reason to expect the difference to go in a particular direction. But it is also possible to do a one-tailed test , where we reject the null hypothesis only if the t score for the sample is extreme in one direction that we specify before collecting the data. This test makes sense when we have good reason to expect the sample mean will differ from the hypothetical population mean in a particular direction.
Here is how it works. Each one-tailed critical value in Table 13.2 can again be interpreted as a pair of values: one positive and one negative. A t score below the lower critical value is in the lowest 5% of the distribution, and a t score above the upper critical value is in the highest 5% of the distribution. For 24 degrees of freedom, these values are −1.711 and +1.711. (These are represented by the green vertical lines in Figure 13.1.) However, for a one-tailed test, we must decide before collecting data whether we expect the sample mean to be lower than the hypothetical population mean, in which case we would use only the lower critical value, or we expect the sample mean to be greater than the hypothetical population mean, in which case we would use only the upper critical value. Notice that we still reject the null hypothesis when the t score for our sample is in the most extreme 5% of the t scores we would expect if the null hypothesis were true—so α remains at .05. We have simply redefined extreme to refer only to one tail of the distribution. The advantage of the one-tailed test is that critical values are less extreme. If the sample mean differs from the hypothetical population mean in the expected direction, then we have a better chance of rejecting the null hypothesis. The disadvantage is that if the sample mean differs from the hypothetical population mean in the unexpected direction, then there is no chance at all of rejecting the null hypothesis.
Example One-Sample t Test
Imagine that a health psychologist is interested in the accuracy of university students’ estimates of the number of calories in a chocolate chip cookie. He shows the cookie to a sample of 10 students and asks each one to estimate the number of calories in it. Because the actual number of calories in the cookie is 250, this is the hypothetical population mean of interest (µ 0 ). The null hypothesis is that the mean estimate for the population (μ) is 250. Because he has no real sense of whether the students will underestimate or overestimate the number of calories, he decides to do a two-tailed test. Now imagine further that the participants’ actual estimates are as follows:
250, 280, 200, 150, 175, 200, 200, 220, 180, 250
The mean estimate for the sample ( M ) is 212.00 calories and the standard deviation ( SD ) is 39.17. The health psychologist can now compute the t score for his sample:
![Rendered by QuickLaTeX.com \[t=\dfrac{212-250}{\left(\dfrac{39.17}{\sqrt{10}}\right)}=-3.07\]](https://opentextbc.ca/researchmethods/wp-content/ql-cache/quicklatex.com-db8519a8464a24c9b7486a9cbd7fdc6b_l3.png)
If he enters the data into one of the online analysis tools or uses SPSS, it would also tell him that the two-tailed p value for this t score (with 10 − 1 = 9 degrees of freedom) is .013. Because this is less than .05, the health psychologist would reject the null hypothesis and conclude that university students tend to underestimate the number of calories in a chocolate chip cookie. If he computes the t score by hand, he could look at Table 13.2 and see that the critical value of t for a two-tailed test with 9 degrees of freedom is ±2.262. The fact that his t score was more extreme than this critical value would tell him that his p value is less than .05 and that he should reject the null hypothesis.
Finally, if this researcher had gone into this study with good reason to expect that university students underestimate the number of calories, then he could have done a one-tailed test instead of a two-tailed test. The only thing this decision would change is the critical value, which would be −1.833. This slightly less extreme value would make it a bit easier to reject the null hypothesis. However, if it turned out that university students overestimate the number of calories—no matter how much they overestimate it—the researcher would not have been able to reject the null hypothesis.
The Dependent-Samples t Test
The dependent-samples t test (sometimes called the paired-samples t test) is used to compare two means for the same sample tested at two different times or under two different conditions. This comparison is appropriate for pretest-posttest designs or within-subjects experiments. The null hypothesis is that the means at the two times or under the two conditions are the same in the population. The alternative hypothesis is that they are not the same. This test can also be one-tailed if the researcher has good reason to expect the difference goes in a particular direction.
It helps to think of the dependent-samples t test as a special case of the one-sample t test. However, the first step in the dependent-samples t test is to reduce the two scores for each participant to a single difference score by taking the difference between them. At this point, the dependent-samples t test becomes a one-sample t test on the difference scores. The hypothetical population mean (µ 0 ) of interest is 0 because this is what the mean difference score would be if there were no difference on average between the two times or two conditions. We can now think of the null hypothesis as being that the mean difference score in the population is 0 (µ 0 = 0) and the alternative hypothesis as being that the mean difference score in the population is not 0 (µ 0 ≠ 0).
Example Dependent-Samples t Test
Imagine that the health psychologist now knows that people tend to underestimate the number of calories in junk food and has developed a short training program to improve their estimates. To test the effectiveness of this program, he conducts a pretest-posttest study in which 10 participants estimate the number of calories in a chocolate chip cookie before the training program and then again afterward. Because he expects the program to increase the participants’ estimates, he decides to do a one-tailed test. Now imagine further that the pretest estimates are
230, 250, 280, 175, 150, 200, 180, 210, 220, 190
and that the posttest estimates (for the same participants in the same order) are
250, 260, 250, 200, 160, 200, 200, 180, 230, 240
The difference scores, then, are as follows:
+20, +10, −30, +25, +10, 0, +20, −30, +10, +50
Note that it does not matter whether the first set of scores is subtracted from the second or the second from the first as long as it is done the same way for all participants. In this example, it makes sense to subtract the pretest estimates from the posttest estimates so that positive difference scores mean that the estimates went up after the training and negative difference scores mean the estimates went down.
The mean of the difference scores is 8.50 with a standard deviation of 27.27. The health psychologist can now compute the t score for his sample as follows:
![Rendered by QuickLaTeX.com \[t=\dfrac{8.5-0}{\left(\dfrac{27.27}{\sqrt{10}}\right)}=1.11\]](https://opentextbc.ca/researchmethods/wp-content/ql-cache/quicklatex.com-37d0f432a138ce195614d7cebaabb4d8_l3.png)
If he enters the data into one of the online analysis tools or uses Excel or SPSS, it would tell him that the one-tailed p value for this t score (again with 10 − 1 = 9 degrees of freedom) is .148. Because this is greater than .05, he would retain the null hypothesis and conclude that the training program does not increase people’s calorie estimates. If he were to compute the t score by hand, he could look at Table 13.2 and see that the critical value of t for a one-tailed test with 9 degrees of freedom is +1.833. (It is positive this time because he was expecting a positive mean difference score.) The fact that his t score was less extreme than this critical value would tell him that his p value is greater than .05 and that he should fail to reject the null hypothesis.
The Independent-Samples t Test
The independent-samples t test is used to compare the means of two separate samples ( M 1 and M 2 ). The two samples might have been tested under different conditions in a between-subjects experiment, or they could be preexisting groups in a correlational design (e.g., women and men, extraverts and introverts). The null hypothesis is that the means of the two populations are the same: µ 1 = µ 2 . The alternative hypothesis is that they are not the same: µ 1 ≠ µ 2 . Again, the test can be one-tailed if the researcher has good reason to expect the difference goes in a particular direction.
The t statistic here is a bit more complicated because it must take into account two sample means, two standard deviations, and two sample sizes. The formula is as follows:
![Rendered by QuickLaTeX.com \[t=\dfrac{M_1-M_2}{\sqrt{\dfrac{{SD_1}^2}{n_1}+\dfrac{{SD_2}^2}{n_2}}}\]](https://opentextbc.ca/researchmethods/wp-content/ql-cache/quicklatex.com-0242d1ab42d68adb3bb852a45bfb9b2d_l3.png)
Notice that this formula includes squared standard deviations (the variances) that appear inside the square root symbol. Also, lowercase n 1 and n 2 refer to the sample sizes in the two groups or condition (as opposed to capital N , which generally refers to the total sample size). The only additional thing to know here is that there are N − 2 degrees of freedom for the independent-samples t test.
Example Independent-Samples t Test
Now the health psychologist wants to compare the calorie estimates of people who regularly eat junk food with the estimates of people who rarely eat junk food. He believes the difference could come out in either direction so he decides to conduct a two-tailed test. He collects data from a sample of eight participants who eat junk food regularly and seven participants who rarely eat junk food. The data are as follows:
Junk food eaters: 180, 220, 150, 85, 200, 170, 150, 190
Non–junk food eaters: 200, 240, 190, 175, 200, 300, 240
The mean for the junk food eaters is 220.71 with a standard deviation of 41.23. The mean for the non–junk food eaters is 168.12 with a standard deviation of 42.66. He can now compute his t score as follows:
![Rendered by QuickLaTeX.com \[t=\dfrac{220.71-168.12}{\sqrt{\dfrac{41.23^2}{8}+\dfrac{42.66^2}{7}}}=2.42\]](https://opentextbc.ca/researchmethods/wp-content/ql-cache/quicklatex.com-8dd797ba37fac6e3618f34946daefb5b_l3.png)
If he enters the data into one of the online analysis tools or uses Excel or SPSS, it would tell him that the two-tailed p value for this t score (with 15 − 2 = 13 degrees of freedom) is .015. Because this p value is less than .05, the health psychologist would reject the null hypothesis and conclude that people who eat junk food regularly make lower calorie estimates than people who eat it rarely. If he were to compute the t score by hand, he could look at Table 13.2 and see that the critical value of t for a two-tailed test with 13 degrees of freedom is ±2.160. The fact that his t score was more extreme than this critical value would tell him that his p value is less than .05 and that he should fail to retain the null hypothesis.
The Analysis of Variance
When there are more than two groups or condition means to be compared, the most common null hypothesis test is the analysis of variance (ANOVA) . In this section, we look primarily at the one-way ANOVA , which is used for between-subjects designs with a single independent variable. We then briefly consider some other versions of the ANOVA that are used for within-subjects and factorial research designs.
One-Way ANOVA
The one-way ANOVA is used to compare the means of more than two samples ( M 1 , M 2 … M G ) in a between-subjects design. The null hypothesis is that all the means are equal in the population: µ 1 = µ 2 =…= µ G . The alternative hypothesis is that not all the means in the population are equal.
The test statistic for the ANOVA is called F . It is a ratio of two estimates of the population variance based on the sample data. One estimate of the population variance is called the mean squares between groups (MS B ) and is based on the differences among the sample means. The other is called the mean squares within groups (MS W ) and is based on the differences among the scores within each group. The F statistic is the ratio of the MS B to the MS W and can therefore be expressed as follows:
F = MS B ÷ MS W
Again, the reason that F is useful is that we know how it is distributed when the null hypothesis is true. As shown in Figure 13.2, this distribution is unimodal and positively skewed with values that cluster around 1. The precise shape of the distribution depends on both the number of groups and the sample size, and there is a degrees of freedom value associated with each of these. The between-groups degrees of freedom is the number of groups minus one: df B = ( G − 1). The within-groups degrees of freedom is the total sample size minus the number of groups: df W = N − G . Again, knowing the distribution of F when the null hypothesis is true allows us to find the p value.
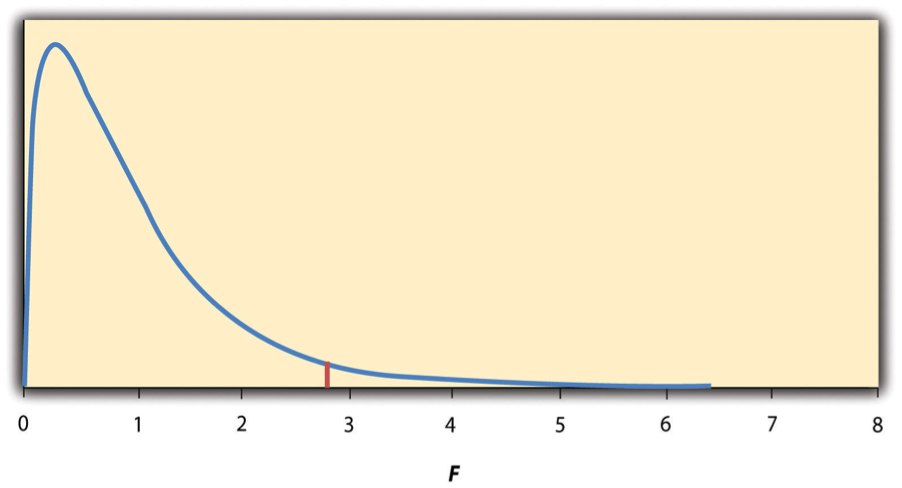
The online tools in Chapter 12 and statistical software such as Excel and SPSS will compute F and find the p value. If p is less than .05, then we reject the null hypothesis and conclude that there are differences among the group means in the population. If p is greater than .05, then we retain the null hypothesis and conclude that there is not enough evidence to say that there are differences. In the unlikely event that we would compute F by hand, we can use a table of critical values like Table 13.3 “Table of Critical Values of ” to make the decision. The idea is that any F ratio greater than the critical value has a p value of less than .05. Thus if the F ratio we compute is beyond the critical value, then we reject the null hypothesis. If the F ratio we compute is less than the critical value, then we retain the null hypothesis.
| 2 | 3 | 4 | |
|---|---|---|---|
| 8 | 4.459 | 4.066 | 3.838 |
| 9 | 4.256 | 3.863 | 3.633 |
| 10 | 4.103 | 3.708 | 3.478 |
| 11 | 3.982 | 3.587 | 3.357 |
| 12 | 3.885 | 3.490 | 3.259 |
| 13 | 3.806 | 3.411 | 3.179 |
| 14 | 3.739 | 3.344 | 3.112 |
| 15 | 3.682 | 3.287 | 3.056 |
| 16 | 3.634 | 3.239 | 3.007 |
| 17 | 3.592 | 3.197 | 2.965 |
| 18 | 3.555 | 3.160 | 2.928 |
| 19 | 3.522 | 3.127 | 2.895 |
| 20 | 3.493 | 3.098 | 2.866 |
| 21 | 3.467 | 3.072 | 2.840 |
| 22 | 3.443 | 3.049 | 2.817 |
| 23 | 3.422 | 3.028 | 2.796 |
| 24 | 3.403 | 3.009 | 2.776 |
| 25 | 3.385 | 2.991 | 2.759 |
| 30 | 3.316 | 2.922 | 2.690 |
| 35 | 3.267 | 2.874 | 2.641 |
| 40 | 3.232 | 2.839 | 2.606 |
| 45 | 3.204 | 2.812 | 2.579 |
| 50 | 3.183 | 2.790 | 2.557 |
| 55 | 3.165 | 2.773 | 2.540 |
| 60 | 3.150 | 2.758 | 2.525 |
| 65 | 3.138 | 2.746 | 2.513 |
| 70 | 3.128 | 2.736 | 2.503 |
| 75 | 3.119 | 2.727 | 2.494 |
| 80 | 3.111 | 2.719 | 2.486 |
| 85 | 3.104 | 2.712 | 2.479 |
| 90 | 3.098 | 2.706 | 2.473 |
| 95 | 3.092 | 2.700 | 2.467 |
| 100 | 3.087 | 2.696 | 2.463 |
Example One-Way ANOVA
Imagine that the health psychologist wants to compare the calorie estimates of psychology majors, nutrition majors, and professional dieticians. He collects the following data:
Psych majors: 200, 180, 220, 160, 150, 200, 190, 200
Nutrition majors: 190, 220, 200, 230, 160, 150, 200, 210, 195
Dieticians: 220, 250, 240, 275, 250, 230, 200, 240
The means are 187.50 ( SD = 23.14), 195.00 ( SD = 27.77), and 238.13 ( SD = 22.35), respectively. So it appears that dieticians made substantially more accurate estimates on average. The researcher would almost certainly enter these data into a program such as Excel or SPSS, which would compute F for him and find the p value. Table 13.4 shows the output of the one-way ANOVA function in Excel for these data. This table is referred to as an ANOVA table. It shows that MS B is 5,971.88, MS W is 602.23, and their ratio, F , is 9.92. The p value is .0009. Because this value is below .05, the researcher would reject the null hypothesis and conclude that the mean calorie estimates for the three groups are not the same in the population. Notice that the ANOVA table also includes the “sum of squares” ( SS ) for between groups and for within groups. These values are computed on the way to finding MS B and MS W but are not typically reported by the researcher. Finally, if the researcher were to compute the F ratio by hand, he could look at Table 13.3 and see that the critical value of F with 2 and 21 degrees of freedom is 3.467 (the same value in Table 13.4 under F crit ). The fact that his F score was more extreme than this critical value would tell him that his p value is less than .05 and that he should reject the null hypothesis.
| Between groups | 11,943.75 | 2 | 5,971.875 | 9.916234 | 0.000928 | 3.4668 |
| Within groups | 12,646.88 | 21 | 602.2321 | |||
| Total | 24,590.63 | 23 |
ANOVA Elaborations
Post hoc comparisons.
When we reject the null hypothesis in a one-way ANOVA, we conclude that the group means are not all the same in the population. But this can indicate different things. With three groups, it can indicate that all three means are significantly different from each other. Or it can indicate that one of the means is significantly different from the other two, but the other two are not significantly different from each other. It could be, for example, that the mean calorie estimates of psychology majors, nutrition majors, and dieticians are all significantly different from each other. Or it could be that the mean for dieticians is significantly different from the means for psychology and nutrition majors, but the means for psychology and nutrition majors are not significantly different from each other. For this reason, statistically significant one-way ANOVA results are typically followed up with a series of post hoc comparisons of selected pairs of group means to determine which are different from which others.
One approach to post hoc comparisons would be to conduct a series of independent-samples t tests comparing each group mean to each of the other group means. But there is a problem with this approach. In general, if we conduct a t test when the null hypothesis is true, we have a 5% chance of mistakenly rejecting the null hypothesis (see Section 13.3 “Additional Considerations” for more on such Type I errors). If we conduct several t tests when the null hypothesis is true, the chance of mistakenly rejecting at least one null hypothesis increases with each test we conduct. Thus researchers do not usually make post hoc comparisons using standard t tests because there is too great a chance that they will mistakenly reject at least one null hypothesis. Instead, they use one of several modified t test procedures—among them the Bonferonni procedure, Fisher’s least significant difference (LSD) test, and Tukey’s honestly significant difference (HSD) test. The details of these approaches are beyond the scope of this book, but it is important to understand their purpose. It is to keep the risk of mistakenly rejecting a true null hypothesis to an acceptable level (close to 5%).
Repeated-Measures ANOVA
Recall that the one-way ANOVA is appropriate for between-subjects designs in which the means being compared come from separate groups of participants. It is not appropriate for within-subjects designs in which the means being compared come from the same participants tested under different conditions or at different times. This requires a slightly different approach, called the repeated-measures ANOVA . The basics of the repeated-measures ANOVA are the same as for the one-way ANOVA. The main difference is that measuring the dependent variable multiple times for each participant allows for a more refined measure of MS W . Imagine, for example, that the dependent variable in a study is a measure of reaction time. Some participants will be faster or slower than others because of stable individual differences in their nervous systems, muscles, and other factors. In a between-subjects design, these stable individual differences would simply add to the variability within the groups and increase the value of MS W . In a within-subjects design, however, these stable individual differences can be measured and subtracted from the value of MS W . This lower value of MS W means a higher value of F and a more sensitive test.
Factorial ANOVA
When more than one independent variable is included in a factorial design, the appropriate approach is the factorial ANOVA . Again, the basics of the factorial ANOVA are the same as for the one-way and repeated-measures ANOVAs. The main difference is that it produces an F ratio and p value for each main effect and for each interaction. Returning to our calorie estimation example, imagine that the health psychologist tests the effect of participant major (psychology vs. nutrition) and food type (cookie vs. hamburger) in a factorial design. A factorial ANOVA would produce separate F ratios and p values for the main effect of major, the main effect of food type, and the interaction between major and food. Appropriate modifications must be made depending on whether the design is between subjects, within subjects, or mixed.

Testing Pearson’s r
For relationships between quantitative variables, where Pearson’s r is used to describe the strength of those relationships, the appropriate null hypothesis test is a test of Pearson’s r . The basic logic is exactly the same as for other null hypothesis tests. In this case, the null hypothesis is that there is no relationship in the population. We can use the Greek lowercase rho (ρ) to represent the relevant parameter: ρ = 0. The alternative hypothesis is that there is a relationship in the population: ρ ≠ 0. As with the t test, this test can be two-tailed if the researcher has no expectation about the direction of the relationship or one-tailed if the researcher expects the relationship to go in a particular direction.
It is possible to use Pearson’s r for the sample to compute a t score with N − 2 degrees of freedom and then to proceed as for a t test. However, because of the way it is computed, Pearson’s r can also be treated as its own test statistic. The online statistical tools and statistical software such as Excel and SPSS generally compute Pearson’s r and provide the p value associated with that value of Pearson’s r . As always, if the p value is less than .05, we reject the null hypothesis and conclude that there is a relationship between the variables in the population. If the p value is greater than .05, we retain the null hypothesis and conclude that there is not enough evidence to say there is a relationship in the population. If we compute Pearson’s r by hand, we can use a table like Table 13.5, which shows the critical values of r for various samples sizes when α is .05. A sample value of Pearson’s r that is more extreme than the critical value is statistically significant.
| Critical value of one-tailed | Critical value of two-tailed | |
|---|---|---|
| 5 | .805 | .878 |
| 10 | .549 | .632 |
| 15 | .441 | .514 |
| 20 | .378 | .444 |
| 25 | .337 | .396 |
| 30 | .306 | .361 |
| 35 | .283 | .334 |
| 40 | .264 | .312 |
| 45 | .248 | .294 |
| 50 | .235 | .279 |
| 55 | .224 | .266 |
| 60 | .214 | .254 |
| 65 | .206 | .244 |
| 70 | .198 | .235 |
| 75 | .191 | .227 |
| 80 | .185 | .220 |
| 85 | .180 | .213 |
| 90 | .174 | .207 |
| 95 | .170 | .202 |
| 100 | .165 | .197 |
Example Test of Pearson’s r
Imagine that the health psychologist is interested in the correlation between people’s calorie estimates and their weight. He has no expectation about the direction of the relationship, so he decides to conduct a two-tailed test. He computes the correlation for a sample of 22 university students and finds that Pearson’s r is −.21. The statistical software he uses tells him that the p value is .348. It is greater than .05, so he retains the null hypothesis and concludes that there is no relationship between people’s calorie estimates and their weight. If he were to compute Pearson’s r by hand, he could look at Table 13.5 and see that the critical value for 22 − 2 = 20 degrees of freedom is .444. The fact that Pearson’s r for the sample is less extreme than this critical value tells him that the p value is greater than .05 and that he should retain the null hypothesis.
Key Takeaways
- To compare two means, the most common null hypothesis test is the t test. The one-sample t test is used for comparing one sample mean with a hypothetical population mean of interest, the dependent-samples t test is used to compare two means in a within-subjects design, and the independent-samples t test is used to compare two means in a between-subjects design.
- To compare more than two means, the most common null hypothesis test is the analysis of variance (ANOVA). The one-way ANOVA is used for between-subjects designs with one independent variable, the repeated-measures ANOVA is used for within-subjects designs, and the factorial ANOVA is used for factorial designs.
- A null hypothesis test of Pearson’s r is used to compare a sample value of Pearson’s r with a hypothetical population value of 0.
- Practice: Use one of the online tools, Excel, or SPSS to reproduce the one-sample t test, dependent-samples t test, independent-samples t test, and one-way ANOVA for the four sets of calorie estimation data presented in this section.
- Practice: A sample of 25 university students rated their friendliness on a scale of 1 ( Much Lower Than Average ) to 7 ( Much Higher Than Average ). Their mean rating was 5.30 with a standard deviation of 1.50. Conduct a one-sample t test comparing their mean rating with a hypothetical mean rating of 4 ( Average ). The question is whether university students have a tendency to rate themselves as friendlier than average.
- The correlation between height and IQ is +.13 in a sample of 35.
- For a sample of 88 university students, the correlation between how disgusted they felt and the harshness of their moral judgments was +.23.
- The correlation between the number of daily hassles and positive mood is −.43 for a sample of 30 middle-aged adults.
A common null hypothesis test examining the difference between two means.
Compares a sample mean with a hypothetical population mean that provides some interesting standard of comparison.
A statistic that is computed only to help find the p value.
Points on the test distribution that are compared to the test statistic to determine whether to reject the null hypothesis.
The null hypothesis is rejected if the t score for the sample is extreme in either direction.
Where the null hypothesis is rejected only if the t score for the sample is extreme in one direction that we specify before collecting the data.
Statistical test used to compare two means for the same sample tested at two different times or under two different conditions.
Variable formed by subtracting one variable from another.
Statistical test used to compare the means of two separate samples.
Most common null hypothesis test when there are more than two groups or condition means to be compared.
A null hypothesis test that is used for between-between subjects designs with a single independent variable.
An estimate of population variance based on the differences among the sample means.
An estimate of population variance based on the differences among the scores within each group.
Analysis of selected pairs of group means to determine which are different from which others.
The dependent variable is measured multiple times for each participant, allowing a more refined measure of MSW.
A null hypothesis test that is used when more than one independent variable is included in a factorial design.
Research Methods in Psychology - 2nd Canadian Edition Copyright © 2015 by Paul C. Price, Rajiv Jhangiani, & I-Chant A. Chiang is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.
Share This Book
Null Hypothesis Definition and Examples
PM Images / Getty Images
- Chemical Laws
- Periodic Table
- Projects & Experiments
- Scientific Method
- Biochemistry
- Physical Chemistry
- Medical Chemistry
- Chemistry In Everyday Life
- Famous Chemists
- Activities for Kids
- Abbreviations & Acronyms
- Weather & Climate
- Ph.D., Biomedical Sciences, University of Tennessee at Knoxville
- B.A., Physics and Mathematics, Hastings College
In a scientific experiment, the null hypothesis is the proposition that there is no effect or no relationship between phenomena or populations. If the null hypothesis is true, any observed difference in phenomena or populations would be due to sampling error (random chance) or experimental error. The null hypothesis is useful because it can be tested and found to be false, which then implies that there is a relationship between the observed data. It may be easier to think of it as a nullifiable hypothesis or one that the researcher seeks to nullify. The null hypothesis is also known as the H 0, or no-difference hypothesis.
The alternate hypothesis, H A or H 1 , proposes that observations are influenced by a non-random factor. In an experiment, the alternate hypothesis suggests that the experimental or independent variable has an effect on the dependent variable .
How to State a Null Hypothesis
There are two ways to state a null hypothesis. One is to state it as a declarative sentence, and the other is to present it as a mathematical statement.
For example, say a researcher suspects that exercise is correlated to weight loss, assuming diet remains unchanged. The average length of time to achieve a certain amount of weight loss is six weeks when a person works out five times a week. The researcher wants to test whether weight loss takes longer to occur if the number of workouts is reduced to three times a week.
The first step to writing the null hypothesis is to find the (alternate) hypothesis. In a word problem like this, you're looking for what you expect to be the outcome of the experiment. In this case, the hypothesis is "I expect weight loss to take longer than six weeks."
This can be written mathematically as: H 1 : μ > 6
In this example, μ is the average.
Now, the null hypothesis is what you expect if this hypothesis does not happen. In this case, if weight loss isn't achieved in greater than six weeks, then it must occur at a time equal to or less than six weeks. This can be written mathematically as:
H 0 : μ ≤ 6
The other way to state the null hypothesis is to make no assumption about the outcome of the experiment. In this case, the null hypothesis is simply that the treatment or change will have no effect on the outcome of the experiment. For this example, it would be that reducing the number of workouts would not affect the time needed to achieve weight loss:
H 0 : μ = 6
Null Hypothesis Examples
"Hyperactivity is unrelated to eating sugar " is an example of a null hypothesis. If the hypothesis is tested and found to be false, using statistics, then a connection between hyperactivity and sugar ingestion may be indicated. A significance test is the most common statistical test used to establish confidence in a null hypothesis.
Another example of a null hypothesis is "Plant growth rate is unaffected by the presence of cadmium in the soil ." A researcher could test the hypothesis by measuring the growth rate of plants grown in a medium lacking cadmium, compared with the growth rate of plants grown in mediums containing different amounts of cadmium. Disproving the null hypothesis would set the groundwork for further research into the effects of different concentrations of the element in soil.
Why Test a Null Hypothesis?
You may be wondering why you would want to test a hypothesis just to find it false. Why not just test an alternate hypothesis and find it true? The short answer is that it is part of the scientific method. In science, propositions are not explicitly "proven." Rather, science uses math to determine the probability that a statement is true or false. It turns out it's much easier to disprove a hypothesis than to positively prove one. Also, while the null hypothesis may be simply stated, there's a good chance the alternate hypothesis is incorrect.
For example, if your null hypothesis is that plant growth is unaffected by duration of sunlight, you could state the alternate hypothesis in several different ways. Some of these statements might be incorrect. You could say plants are harmed by more than 12 hours of sunlight or that plants need at least three hours of sunlight, etc. There are clear exceptions to those alternate hypotheses, so if you test the wrong plants, you could reach the wrong conclusion. The null hypothesis is a general statement that can be used to develop an alternate hypothesis, which may or may not be correct.
- Kelvin Temperature Scale Definition
- Independent Variable Definition and Examples
- Theory Definition in Science
- Hypothesis Definition (Science)
- de Broglie Equation Definition
- Law of Combining Volumes Definition
- Chemical Definition
- Pure Substance Definition in Chemistry
- Acid Definition and Examples
- Extensive Property Definition (Chemistry)
- Radiation Definition and Examples
- Valence Definition in Chemistry
- Atomic Solid Definition
- Weak Base Definition and Examples
- Oxidation Definition and Example in Chemistry
- Definition of Binary Compound
- Math Article
Null Hypothesis

In mathematics, Statistics deals with the study of research and surveys on the numerical data. For taking surveys, we have to define the hypothesis. Generally, there are two types of hypothesis. One is a null hypothesis, and another is an alternative hypothesis .
In probability and statistics, the null hypothesis is a comprehensive statement or default status that there is zero happening or nothing happening. For example, there is no connection among groups or no association between two measured events. It is generally assumed here that the hypothesis is true until any other proof has been brought into the light to deny the hypothesis. Let us learn more here with definition, symbol, principle, types and example, in this article.
Table of contents:
- Comparison with Alternative Hypothesis
Null Hypothesis Definition
The null hypothesis is a kind of hypothesis which explains the population parameter whose purpose is to test the validity of the given experimental data. This hypothesis is either rejected or not rejected based on the viability of the given population or sample . In other words, the null hypothesis is a hypothesis in which the sample observations results from the chance. It is said to be a statement in which the surveyors wants to examine the data. It is denoted by H 0 .
Null Hypothesis Symbol
In statistics, the null hypothesis is usually denoted by letter H with subscript ‘0’ (zero), such that H 0 . It is pronounced as H-null or H-zero or H-nought. At the same time, the alternative hypothesis expresses the observations determined by the non-random cause. It is represented by H 1 or H a .
Null Hypothesis Principle
The principle followed for null hypothesis testing is, collecting the data and determining the chances of a given set of data during the study on some random sample, assuming that the null hypothesis is true. In case if the given data does not face the expected null hypothesis, then the outcome will be quite weaker, and they conclude by saying that the given set of data does not provide strong evidence against the null hypothesis because of insufficient evidence. Finally, the researchers tend to reject that.
Null Hypothesis Formula
Here, the hypothesis test formulas are given below for reference.
The formula for the null hypothesis is:
H 0 : p = p 0
The formula for the alternative hypothesis is:
H a = p >p 0 , < p 0 ≠ p 0
The formula for the test static is:
Remember that, p 0 is the null hypothesis and p – hat is the sample proportion.
Also, read:
Types of Null Hypothesis
There are different types of hypothesis. They are:
Simple Hypothesis
It completely specifies the population distribution. In this method, the sampling distribution is the function of the sample size.
Composite Hypothesis
The composite hypothesis is one that does not completely specify the population distribution.
Exact Hypothesis
Exact hypothesis defines the exact value of the parameter. For example μ= 50
Inexact Hypothesis
This type of hypothesis does not define the exact value of the parameter. But it denotes a specific range or interval. For example 45< μ <60
Null Hypothesis Rejection
Sometimes the null hypothesis is rejected too. If this hypothesis is rejected means, that research could be invalid. Many researchers will neglect this hypothesis as it is merely opposite to the alternate hypothesis. It is a better practice to create a hypothesis and test it. The goal of researchers is not to reject the hypothesis. But it is evident that a perfect statistical model is always associated with the failure to reject the null hypothesis.
How do you Find the Null Hypothesis?
The null hypothesis says there is no correlation between the measured event (the dependent variable) and the independent variable. We don’t have to believe that the null hypothesis is true to test it. On the contrast, you will possibly assume that there is a connection between a set of variables ( dependent and independent).
When is Null Hypothesis Rejected?
The null hypothesis is rejected using the P-value approach. If the P-value is less than or equal to the α, there should be a rejection of the null hypothesis in favour of the alternate hypothesis. In case, if P-value is greater than α, the null hypothesis is not rejected.
Null Hypothesis and Alternative Hypothesis
Now, let us discuss the difference between the null hypothesis and the alternative hypothesis.
|
|
| |
| 1 | The null hypothesis is a statement. There exists no relation between two variables | Alternative hypothesis a statement, there exists some relationship between two measured phenomenon |
| 2 | Denoted by H | Denoted by H |
| 3 | The observations of this hypothesis are the result of chance | The observations of this hypothesis are the result of real effect |
| 4 | The mathematical formulation of the null hypothesis is an equal sign | The mathematical formulation alternative hypothesis is an inequality sign such as greater than, less than, etc. |
Null Hypothesis Examples
Here, some of the examples of the null hypothesis are given below. Go through the below ones to understand the concept of the null hypothesis in a better way.
If a medicine reduces the risk of cardiac stroke, then the null hypothesis should be “the medicine does not reduce the chance of cardiac stroke”. This testing can be performed by the administration of a drug to a certain group of people in a controlled way. If the survey shows that there is a significant change in the people, then the hypothesis is rejected.
Few more examples are:
1). Are there is 100% chance of getting affected by dengue?
Ans: There could be chances of getting affected by dengue but not 100%.
2). Do teenagers are using mobile phones more than grown-ups to access the internet?
Ans: Age has no limit on using mobile phones to access the internet.
3). Does having apple daily will not cause fever?
Ans: Having apple daily does not assure of not having fever, but increases the immunity to fight against such diseases.
4). Do the children more good in doing mathematical calculations than grown-ups?
Ans: Age has no effect on Mathematical skills.
In many common applications, the choice of the null hypothesis is not automated, but the testing and calculations may be automated. Also, the choice of the null hypothesis is completely based on previous experiences and inconsistent advice. The choice can be more complicated and based on the variety of applications and the diversity of the objectives.
The main limitation for the choice of the null hypothesis is that the hypothesis suggested by the data is based on the reasoning which proves nothing. It means that if some hypothesis provides a summary of the data set, then there would be no value in the testing of the hypothesis on the particular set of data.
Frequently Asked Questions on Null Hypothesis
What is meant by the null hypothesis.
In Statistics, a null hypothesis is a type of hypothesis which explains the population parameter whose purpose is to test the validity of the given experimental data.
What are the benefits of hypothesis testing?
Hypothesis testing is defined as a form of inferential statistics, which allows making conclusions from the entire population based on the sample representative.
When a null hypothesis is accepted and rejected?
The null hypothesis is either accepted or rejected in terms of the given data. If P-value is less than α, then the null hypothesis is rejected in favor of the alternative hypothesis, and if the P-value is greater than α, then the null hypothesis is accepted in favor of the alternative hypothesis.
Why is the null hypothesis important?
The importance of the null hypothesis is that it provides an approximate description of the phenomena of the given data. It allows the investigators to directly test the relational statement in a research study.
How to accept or reject the null hypothesis in the chi-square test?
If the result of the chi-square test is bigger than the critical value in the table, then the data does not fit the model, which represents the rejection of the null hypothesis.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!
Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz
Visit BYJU’S for all Maths related queries and study materials
Your result is as below
Request OTP on Voice Call
| MATHS Related Links | |
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.
- Search Search Please fill out this field.
What Is a Null Hypothesis?
The alternative hypothesis.
- Additional Examples
- Null Hypothesis and Investments
The Bottom Line
- Corporate Finance
- Financial Ratios
Null Hypothesis: What Is It, and How Is It Used in Investing?
Adam Hayes, Ph.D., CFA, is a financial writer with 15+ years Wall Street experience as a derivatives trader. Besides his extensive derivative trading expertise, Adam is an expert in economics and behavioral finance. Adam received his master's in economics from The New School for Social Research and his Ph.D. from the University of Wisconsin-Madison in sociology. He is a CFA charterholder as well as holding FINRA Series 7, 55 & 63 licenses. He currently researches and teaches economic sociology and the social studies of finance at the Hebrew University in Jerusalem.
:max_bytes(150000):strip_icc():format(webp)/adam_hayes-5bfc262a46e0fb005118b414.jpg)
A null hypothesis is a type of statistical hypothesis that proposes that no statistical significance exists in a set of given observations. Hypothesis testing is used to assess the credibility of a hypothesis by using sample data. Sometimes referred to simply as the “null,” it is represented as H 0 .
The null hypothesis, also known as “the conjecture,” is used in quantitative analysis to test theories about markets, investing strategies, and economies to decide if an idea is true or false.
Key Takeaways
- A null hypothesis is a type of conjecture in statistics that proposes that there is no difference between certain characteristics of a population or data-generating process.
- The alternative hypothesis proposes that there is a difference.
- Hypothesis testing provides a method to reject a null hypothesis within a certain confidence level.
- If you can reject the null hypothesis, it provides support for the alternative hypothesis.
- Null hypothesis testing is the basis of the principle of falsification in science.
Alex Dos Diaz / Investopedia
Understanding a Null Hypothesis
A gambler may be interested in whether a game of chance is fair. If it is, then the expected earnings per play come to zero for both players. If it is not, then the expected earnings are positive for one player and negative for the other.
To test whether the game is fair, the gambler collects earnings data from many repetitions of the game, calculates the average earnings from these data, then tests the null hypothesis that the expected earnings are not different from zero.
If the average earnings from the sample data are sufficiently far from zero, then the gambler will reject the null hypothesis and conclude the alternative hypothesis—namely, that the expected earnings per play are different from zero. If the average earnings from the sample data are near zero, then the gambler will not reject the null hypothesis, concluding instead that the difference between the average from the data and zero is explainable by chance alone.
A null hypothesis can only be rejected, not proven.
The null hypothesis assumes that any kind of difference between the chosen characteristics that you see in a set of data is due to chance. For example, if the expected earnings for the gambling game are truly equal to zero, then any difference between the average earnings in the data and zero is due to chance.
Analysts look to reject the null hypothesis because doing so is a strong conclusion. This requires evidence in the form of an observed difference that is too large to be explained solely by chance. Failing to reject the null hypothesis—that the results are explainable by chance alone—is a weak conclusion because it allows that while factors other than chance may be at work, they may not be strong enough for the statistical test to detect them.
An important point to note is that we are testing the null hypothesis because there is an element of doubt about its validity. Whatever information that is against the stated null hypothesis is captured in the alternative (alternate) hypothesis (H 1 ).
For the examples below, the alternative hypothesis would be:
- Students score an average that is not equal to seven.
- The mean annual return of a mutual fund is not equal to 8% per year.
In other words, the alternative hypothesis is a direct contradiction of the null hypothesis.
Null Hypothesis Examples
Here is a simple example: A school principal claims that students in her school score an average of seven out of 10 in exams. The null hypothesis is that the population mean is not 7.0. To test this null hypothesis, we record marks of, say, 30 students ( sample ) from the entire student population of the school (say, 300) and calculate the mean of that sample.
We can then compare the (calculated) sample mean to the (hypothesized) population mean of 7.0 and attempt to reject the null hypothesis. (The null hypothesis here—that the population mean is not 7.0—cannot be proved using the sample data. It can only be rejected.)
Take another example: The annual return of a particular mutual fund is claimed to be 8%. Assume that the mutual fund has been in existence for 20 years. The null hypothesis is that the mean return is not 8% for the mutual fund. We take a random sample of annual returns of the mutual fund for, say, five years (sample) and calculate the sample mean. We then compare the (calculated) sample mean to the (claimed) population mean (8%) to test the null hypothesis.
For the above examples, null hypotheses are:
- Example A: Students in the school don’t score an average of seven out of 10 in exams.
- Example B: The mean annual return of the mutual fund is not 8% per year.
For the purposes of determining whether to reject the null hypothesis (abbreviated H0), said hypothesis is assumed, for the sake of argument, to be true. Then the likely range of possible values of the calculated statistic (e.g., the average score on 30 students’ tests) is determined under this presumption (e.g., the range of plausible averages might range from 6.2 to 7.8 if the population mean is 7.0).
If the sample average is outside of this range, the null hypothesis is rejected. Otherwise, the difference is said to be “explainable by chance alone,” being within the range that is determined by chance alone.
How Null Hypothesis Testing Is Used in Investments
As an example related to financial markets, assume Alice sees that her investment strategy produces higher average returns than simply buying and holding a stock . The null hypothesis states that there is no difference between the two average returns, and Alice is inclined to believe this until she can conclude contradictory results.
Refuting the null hypothesis would require showing statistical significance, which can be found by a variety of tests. The alternative hypothesis would state that the investment strategy has a higher average return than a traditional buy-and-hold strategy.
One tool that can determine the statistical significance of the results is the p-value. A p-value represents the probability that a difference as large or larger than the observed difference between the two average returns could occur solely by chance.
A p-value that is less than or equal to 0.05 often indicates whether there is evidence against the null hypothesis. If Alice conducts one of these tests, such as a test using the normal model, resulting in a significant difference between her returns and the buy-and-hold returns (the p-value is less than or equal to 0.05), she can then reject the null hypothesis and conclude the alternative hypothesis.
How Is the Null Hypothesis Identified?
The analyst or researcher establishes a null hypothesis based on the research question or problem they are trying to answer. Depending on the question, the null may be identified differently. For example, if the question is simply whether an effect exists (e.g., does X influence Y?), the null hypothesis could be H 0 : X = 0. If the question is instead, is X the same as Y, the H 0 would be X = Y. If it is that the effect of X on Y is positive, H 0 would be X > 0. If the resulting analysis shows an effect that is statistically significantly different from zero, the null can be rejected.
How Is Null Hypothesis Used in Finance?
In finance , a null hypothesis is used in quantitative analysis. It tests the premise of an investing strategy, the markets, or an economy to determine if it is true or false.
For instance, an analyst may want to see if two stocks, ABC and XYZ, are closely correlated. The null hypothesis would be ABC ≠ XYZ.
How Are Statistical Hypotheses Tested?
Statistical hypotheses are tested by a four-step process . The first is for the analyst to state the two hypotheses so that only one can be right. The second is to formulate an analysis plan, which outlines how the data will be evaluated. The third is to carry out the plan and physically analyze the sample data. The fourth and final step is to analyze the results and either reject the null hypothesis or claim that the observed differences are explainable by chance alone.
What Is an Alternative Hypothesis?
An alternative hypothesis is a direct contradiction of a null hypothesis. This means that if one of the two hypotheses is true, the other is false.
A null hypothesis states there is no difference between groups or relationship between variables. It is a type of statistical hypothesis and proposes that no statistical significance exists in a set of given observations. “Null” means nothing.
The null hypothesis is used in quantitative analysis to test theories about economies, investing strategies, and markets to decide if an idea is true or false. Hypothesis testing assesses the credibility of a hypothesis by using sample data. It is represented as H 0 and is sometimes simply known as “the null.”
Sage Publishing. “ Chapter 8: Introduction to Hypothesis Testing ,” Page 4.
Sage Publishing. “ Chapter 8: Introduction to Hypothesis Testing ,” Pages 4 to 7.
Sage Publishing. “ Chapter 8: Introduction to Hypothesis Testing ,” Page 7.
:max_bytes(150000):strip_icc():format(webp)/Term-Definitions_p-value-61f80de6ec3f4bc481ce22dac498109c.png)
- Terms of Service
- Editorial Policy
- Privacy Policy
Forecasting Water Levels in Krasnodar Krai Rivers with the Use of Machine Learning
- WATER RESOURCES AND THE REGIME OF WATER BODIES
- Open access
- Published: 05 March 2022
- Volume 49 , pages 10–22, ( 2022 )
Cite this article
You have full access to this open access article

- P. A. Belyakova 1 , 2 ,
- V. M. Moreido 1 ,
- A. S. Tsyplenkov 3 ,
- A. N. Amerbaev 1 ,
- D. A. Grechishnikova 3 ,
- L. S. Kurochkina 4 ,
- V. A. Filippov 5 &
- M. S. Makeev 6
2215 Accesses
3 Citations
Explore all metrics
The potential of construction of machine learning models was considered as applied to water level forecasting in mountain river reaches in Krasnodar Krai based on observation data on water levels at automated hydrological complexes of the Automated System of Flood Conditions Monitoring in Krasnodar Krai. The study objects were two mountain rivers in Krasnodar Krai―the Pshish and Mzymta. These rivers flow in different natural conditions and differ in their water regimes and the character of lateral inflow in the reaches under consideration. The study focused on three widely used machine learning architectures: regression model of decision trees M5P, gradient boosting of decision trees XGBoost, and artificial neural network based on multilayer perceptron. The forecast quality was evaluated for lead time from 1 to 20 h; variations for rivers with different water regimes and the potential of the examined models as applied to operational forecasting are discussed. The optimal lead time for the Pshish river was found to be 15–18 h (with S/ σ Δ varying within 0.38–0.39 for XGBoost model); the simulation quality for the Mzymta river is evaluated as good; however, the necessary forecast efficiency is not attained (at the lead time of 5 h, we have S/ σ Δ = 0.87 for MLP model). The obtained results allow the machine learning models to be regarded as acceptable for short-term hydrological forecasting based on high-frequency water level observation data.
Similar content being viewed by others
Estimation of hourly flood hydrograph from daily flows using machine learning techniques in the Büyük Menderes River
Floodplain Lake Water Level Prediction with Strong River-Lake Interaction Using the Ensemble Learning LightGBM

Application of Machine Learning Algorithms for Local Level Flood Prediction: A Simplest Way of Likelihood Predictive Model of Monsoon River Flood
Explore related subjects.
- Artificial Intelligence
Avoid common mistakes on your manuscript.
INTRODUCTION
Floods are among the most destructive natural disasters both in Russia and in the World, and their forecasting is a key factor in the protection of the population and economy from floods. In Russia, flood casualties occur every year, and since the early 2000s, more than 80% of people were killed by floods of rain origin and more than 50%, by flash floods [ 2 ]. To ensure the forecast advance time required for emergency services to respond and to alert the population in the case of flood hazard, the system of hydrological forecast is to be developed basing on monitoring data, up-to-date forecast methods, and skilled staff [ 6 , 29 ].
Under current climate changes, the frequency and the scale of hazardous meteorological phenomena, including extreme storm rainfalls, are expected to increase in many regions of the world, thus making the problem of flood forecasting extremely hard at any time scale [ 22 , 25 , 27 ]. In Russia, the contribution of heavy showers to the total precipitation has been also increasing in the recent years [ 21 ].
The progress in forecasting flash floods can be engaged through increasing the availability of data (from gaging stations, the population, and remote sensing) and methods of their effective use, with the aim to improve the understanding of hydrometeorological phenomena and their socioeconomic effects [ 38 ]. In the Krasnodar Krai, a unique for Russia regional automated monitoring system for flood situation (AMSFS KK) has been operating since 2013, including more than 250 automated hydrological complexes (AHC) and more than 90 automated meteorological stations (AMS). Automated gages measure water level in rivers with a frequency of once in 10 min, along with some other weather characteristics, and transmit the data on a real-time basis to the information server of the system through cellular communication channels based on technologies of Emercit company [ 12 ]. Advantages of the system are the high density of the monitoring network (<170 km 2 per 1 AHC in the mountain part of the territory), the high frequency of data transmission, and their open-access in the Internet, emphasizing its significance in ensuring online monitoring of floods and alerting the population about floods. AMSFS KK fits well into the international practice of developing local hydrometeorological systems for solving monitoring problems and flash floods forecasting [ 46 ]. At the same time, the array of high-frequency data acquired by the regional monitoring system can be used to develop methods for simulating and forecasting flash floods. Notwithstanding the relatively short operation period of the Emercit system, measurement results are being actively used by researchers to study hydrological and geomorphological phenomena [ 5 , 13 , 14 ].
The achievements in the field of artificial intelligence (AI) and machine learning (ML) [ 23 , 31 , 32 , 40 ] provide promising methods for incorporating the full potential of large datasets for the analysis and forecasts with the aim to provide accurate and timely data to stakeholders, the population, and the authorities.
The problems of short-term hydrological forecasting often require not detailed description of the processes of runoff formation but an accurate description of the response of the river system to meteorological forcing data [ 17 ]. This is done with the use of simplified models relating previously observed weather and river flow with the future river flow by effectively incorporating the (auto)correlation of time series [ 4 ].
The problem of forecasting water levels in the mountain rivers in Krasnodar Krai is of great importance because of the frequent floods. Water levels are characteristics that can be measured more accurately and easily than water discharges, especially in mountain rivers, and forecasting water levels at a downstream gage of a river reach, considering the observations at the upstream gage is a common hydrological task. The objective of this study is to construct machine learning models for forecasting water levels in the rivers of Pshish (at Guriiskaya Vil.) and Mzymta (at Kazachii Brod Vil.) in Krasnodar Krai, using data on water levels at upstream gages. For the first time we use initial dataset containing high frequency water level observation data on the AMSFS KK network. We employ the three widely used ML model architectures for model construction, i.e., decision tree regression model M5P [ 37 ], gradient boosting of decision trees XGBoost [ 20 ], and an artificial neural network based on multilayer perceptron (hereafter, MLP [ 24 ]). The forecasting effectiveness is tested for the forecast lead time from 1 to 20 h.
STUDY OBJECT
The catchments of the Pshish and Mzymta rivers ( Fig. 1 ) lie on different macroslopes of the Western Caucasus. These rivers were chosen because of their similar catchment sizes ( Table 1 ) and contrast natural conditions in their catchments. The Pshish River is a tributary of the Kuban in its middle reaches; it contributes to the Krasnodar Reservoir. The Mzymta basin lies in the southern Russian part of the Black Sea coast at the Caucasus. This river flows into the Black Sea. The upper reaches of the Mzymta lie further westward in a higher part of the Greater Caucasus; the maximum elevation in the basin is >3250 m, while that on the ridges of the Pshish River catchment is as little as 1800 m. The relief and elevation of the catchments determine their climate features, snow accumulation regime, and the water regime of rivers.
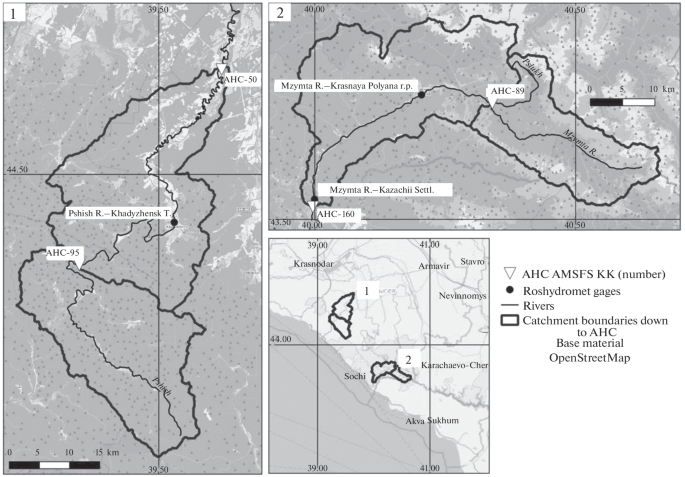
Schematic map of the catchments of (1) the Pshish and (2) Mzymta rivers and the layout of the chosen AHCs.
The Pshish River catchment lies in the zone of temperate climate with annual precipitation >900 mm (with 950 mm in Khadyzhensk T., and 1660 mm in Gornyi Vil.), the snow cover is intermittent. The Mzymta R. basin lies in the zone of humid subtropical climate with an annual rainfall of >1300 mm (1377 mm in Adler City, 1795 mm in Krasnaya Polyana Town) [ 10 ]. Part of the catchment above 600–1300 m belongs to the zone of seasonal snow cover, where snow falls every year and lies during >120 days, thus enabling the operation of ski resorts on the slopes of the Mzymta valley.
According to P.S. Kuzin’s classification [ 7 ], the Pshish is a river with rain floods occurring all year round, though more frequent in the cold season, while the Mzymta is a river with spring–summer freshets and rain floods in all other seasons. The mean maximal level increase in the Pshish R. is 2.9 m at AGK-95 and 6.1 m at AGK-50. The mean rate of level rise during freshets is 0.1–0.6, and maximum of 1.1 m/h. The concentration time between the peaks of high floods in the Pshish River varies from 18 to 28 h, which corresponds to the flood wave propagation velocity of 3−4 m/s in this river reach.
The range of level variations in the Mzymta R. during flood events is 2–3 m. The rate of level rise is commonly relatively low in the upper reaches (0.05–0.24 m/h), while that in the lower reaches is higher―up to 0.5 m/h. In the lower reaches, flood formation often begins earlier because of damp air moving from the sea [ 1 ]. Peak levels can also occur earlier in the lower gage. A definitive case is the flood of June 25, 2015, when showers caused floods on rivers in the coastal zone and in low mountains; at Kazachii Brod, the flood peak passed at 1 p.m., and air masses rose into the mountain part a day later and formed a flood peak at the confluence of the Mzymta and Pslukh rivers at 10 a.m. on June 26.
Notwithstanding the relatively short operation period of AMSFS KK, its sensors have already recorded extreme water level rises, during the flood on October 24–25, 2018, the level rise in the Pshish R. was >6.2 m near Navaginskoe Vil. and 9.3 m at Guriiskaya Vil. According to data of Roshydromet gages for Khadyzhensk T. and Bzhedukhovskaya Vil., this was the highest flood over the observation period since 1936. On the same dates of October 24–25, 2018, a high flood was developing in the Mzymta R. with level rises by 2.0–3.1 m upstream of the confluence with the Pslukh R. and at Kazachii Brod Vil. In the area near Kazachii Brod, this flood ranked second in magnitude after that of October 25, 2003 (or third, taking into account the highest flood recorded on the gage at Kepsha Station on June 26, 1956) during the period of instrumental observations.
Available Hydrometeorological Data
In the chosen rivers, observations on AMSFS KK network are carried out in parallel to observations at Roshydromet gages, thus enabling mutual quality control of the obtained data. The regional AMSFS KKnetwork includes 3 AHCs on the Mzymta R. and 3 AHCs on its tributaries. On the Pshish River and its tributaries, 6 and 2 AHCs are now in operation, respectively. In this study, two pairs of AHC AMSFS KK were chosen at each river with the most complete observation series (with few gaps and outliers) observation series ( Table 1 ). The distance between those gages is 86.5 km along the Pshish R. and 40 km along the Mzymta R.
Processing Data of Water Level Measurements, Removal of Spikes, and Filter Tuning to Reduce Noise in the Series
The study uses the archive dataset of 10-min water level measurements at AHC-95, AHC-50, AHC-89, and AHC- 160 from April 2014 to January 2021.
Due to the design features of the measuring radar sensor and high measurement frequency the time-series are noisy and contain numerous outliers. The majority of the existing procedures used to analyze time series for outliers, spikes, or anomalies are unsuitable for the analysis of water level variations in small mountain rivers because of the specifics of their hydrological regime. The abrupt and fast water level rises, typical for West Caucasian rivers, analyzed with the use of statistical tests known to the authors (Chauvenet’s statistical criterion, Grubbs’s test, Pearse’s test, Dixon’s Q-test) rejected the null hypothesis assuming that the values considered are not outliers. Therefore, the following algorithm has been developed to remove such values caused by measurement errors. First, the regular measurement interval of 10 min was introduced. Next the series was analyzed to identify outliers through revealing events in which water level rose by >1.5 m within 10 min and next dropped by >40 cm. The proportion of outliers at selected AHC varied from 0.05 (18–25 values, associated with sensor calibrations, according to data of JSC Emersit) to 0.24%. Within the 7 years of sensor operation, the proportion of gaps varied from 2.29 to 7.77% of series length. The identified erroneous data were removed, and the gaps were filled by linear interpolation.
After the determination of outliers and the restoration of a regular measurement step, the data were filtered to remove high-frequency noise, typical for this kind of data. The methods of linear and nonlinear filtration [ 39 ] are not suitable for this problem, because they largely reduce the actual range of level variations during floods. Therefore, this was made by Savitzky–Golay smoothing method [ 42 ], which is widely used to process high-frequency observation data in various fields [ 28 , 45 ]. A distinctive feature of this filter is the ability to smooth noises and to preserve the actual variation amplitude [ 36 ]. The smoothing is carried out using 41 samples wide rolling window with 8th degree polynomial. It is followed by linear interpolation aimed to fill in the small gaps <8 h that form due to the removal of outliers and faulty measurements. This is necessary to obtain the most complete series for further modeling.
Preparation of Dataset for Experiments
Matrices of data from 2014 to 2020 were prepared for computation experiments. The calculations were made for a step of 1 h; therefore, before their use, the data were converted to a one-hour step. For each hour, water level was forecasted with some lead time based on the data available at the moment of forecast. The datasets included a set of 54 predictors, i.e., water level series obtained by processing the initial AMSFS KK data. The same dataset contained 8 predicates―series of the forecasted characteristic (water level) with a lead time from 1 to 20 h (the future water levels L t+ 1 , L t+ 2 , L t+ 3 , L t+ 5 , L t+ 10 , L t+ 15 , L t+ 18 , L t+ 20 ).
The predictors included:
water levels at the upstream gage H t- τ (m) at the moment of forecasting and for the previous period τ = 1…48 h;
water levels at the downstream gage L t- τ (m) at the moment of forecasting and for the previous period τ = 1…24 h.
The construction of this dataset allows to account for flood wave routing time along the river channel. The initial datasets are arranged by rows. The data in the first position of each row are the date and the hour t for which the experimental forecast is made.
Next the series of water levels were divided into the training and testing samples according to the recommendations [ 18 ] with a sufficient length and similar statistical characteristics. The training period for the Pshish River was chosen from March 3, 2015, to August 31, 2018 (70% of the data), and the testing period was from September 1, 2018, to January 5, 2020 (30%). The respective periods for the Mzymta were from January 1, 2014, to August 31, 2018 (teaching, 80%) and from September 1, 2018, to January 5, 2020 (check, 20% because of gaps).
THE MODELS AND THE METHODS OF THEIR CONSTRUCTION
Description of m5r model.
The algorithm M5R is based on the algorithm of construction of regression model trees M5 [ 37 ]. This algorithm includes three stages. At the first stage a decision tree is constructed, where the splitting criterion minimizes the variations of predicate values in each branch. At the second stage, truncation is made at each leaf. At the truncation, the inner nodes of the tree form a regression plane. At the third stage, to prevent the formation of breaks, a smoothing procedure is applied. It combines the forecasts of the model in a leaf with the values for each leaf toward the root of the decision tree. An advantage of the algorithm is its compactness and the relatively simple interpretation of the obtained models. The algorithm uses unscaled initial data.
Description of XGBoost Model
XGBoost is gradient boosting of decision trees. Boosting is a technique that helps successively constructing the composition of algorithms; in this case, each new algorithm is constructed in order to minimize the errors of the previous one. The base algorithms of the composition are shallow decision trees.
Suppose we have a composition of N – 1 decision trees:
At the next step, we have to add an algorithm \({{b}_{N}}(x)\) that will decrease the composition error on the learning sample. In other words, we have to determine which values \({{s}_{1}}, \ldots .,{{s}_{t}}\) are to be taken by algorithm \({{b}_{N}}({{x}_{i}}) = {{s}_{i}}\) on the objects of the learning sample for the error of the entire composition to be minimal:
Now, the vector s can be sought for as the antigradient of the error function:
Therefore, training the algorithm \({{b}_{N}}(x)\) is the minimization of the quadratic error function of algorithm responses and elements of vector s .
The model is written in Python language. Library xgboost, version 0.90, was used for the construction. Library sklearn was used to validate the model. The input data for the model were standardized variables within the range [–1; 1].
Description of MLP Model
The neural network model commonly used for hydrological problems [ 16 , 33 , 43 ] is multilayer perceptron MLP [ 24 ]. This is a computation network consisting of artificial neurons, simulating brain neurons. A mathematical model of neuron was first proposed in [ 30 ], however, it started rapidly developing only after the introduction of backpropagation algorithm [ 41 ] for evaluating model parameters (the weights of the input variables). Multilayer perceptron model is based on the use of a single or several layers of artificial neurons, which receive many observation data series on their inputs (for example, water levels with different time shifts) and transform them into an output signal (for example, water levels with a specified lead time) through nonlinear transformations and combinations of input signals with various weights. Mathematically, the artificial neuron can be represented by the dependence
relating the output signal y with a vector of input data \({{x}_{i}}\) ( i = 1, 2, …n ), which enter the model with different weights \({{w}_{i}}\) , and neuron activation threshold b via activation function \({{\varphi }}\) . The activation function is commonly represented by a nonlinear sigmoid function of the form:
The weights with which the vectors of source data enter the artificial neural network were determined based on the comparison of the output signal with the learning vector (observation data) and back propagation, which leads to repeated weighing. This process is referred to as learning a neural network. The learning process is to minimize the chosen error function, which is commonly the root-mean-square deviation (though any other function can be chosen).
The nonlinear relationships established between ANN input and output, as well as the use of any other input data for automated search for model structure allows ANN to be used in various problems, not limited to hydrology. In terms of the structure of hydrological models, ANN is a classical black box model [ 19 ]. Such model does not require a detailed description of the system to be simulated (in our case, the processes of runoff formation in a river basin) for identifying relationships between its inputs and outputs. An advantage of ANN, as applied to complex nonlinear systems, over models with distributed parameters is their less strict requirements to input data. The initial data for the model are standardized characteristics varying within the range [–1; 1].
The process of ANN model development consists of the following. The measurement data used to develop the model are divided into two groups: training and testing. First, the ANN model is trained on the first set of data, and the simulation result is compared with observation data to evaluate simulation quality. Next, the model is tested on an independent dataset under a specified condition regarding the admissible decrease in model quality. The model thus developed and trained can yield an output signal whatever the amount of input data.
The model for forecasting water level variations based on measurement data from AHC AMSFS KK was developed with the use of software components of scikit-learn library of Python language [ 35 ]; the regression problems with training were solved with the use of MLPRegressor software. The main parameters of the model are the number of its hidden layers, the number of neurons in them, the form of the activation function, the algorithm used to search for the global minimum of the optimization function, and the maximal number of iterations. The models’ hyperparameters were optimized by grid search algorithm with ten-fold cross-validation (the training data set is randomly divided into 10 parts, of which 9 are used for parameter tuning and 1 is used for testing; next the dataset is divided in another way; this test is repeated 10 times). These procedures are also implemented as functions of scikit-learn library.
The Methods Used to Evaluate Model Quality
We used the following metrics to evaluate the models’ performance. The root-mean-square error of the simulated values from the observed was calculated using the formula
here \(H_{i}^{{{\text{sim}}}}\) is the simulated water level, m; \(H_{i}^{{{\text{obs}}}}\) is the observed water level; N is the length of the series.
The Nash–Sutcliffe model efficiency coefficient NSE [ 34 ]:
The Nash–Sutcliffe coefficient NSE vary within the range \(\left( { - \infty ;1} \right]\) , at NSE > 0.75, the simulation quality is excellent, at 0.36 < NSE < 0.75, it is satisfactory; and at NSE < 0.36, unsatisfactory.
The quality of the tendency forecast of the models was evaluated by the characteristic S/ σ Δ [4, 9], where σ Δ is the deviation of the inertial forecast for each lead time:
The values of S /σ Δ vary within the range \(\left[ {0; + \infty } \right)\) , with the values of 0–0.5 implying excellent; 0.5–0.7, good; 0.7–0.8, satisfactory; and >1, unsatisfactory quality of the forecast procedure.
It is worth mentioning that the metrics given above are commonly used to evaluate the quality of simulation and forecasting water discharges; however, they can be used for water levels as well.
In the machine learning models that incorporate linear regression, in our case, M5P and XGBoost, the degree of association of predictors and the predicate often determines the quality of modeling and can be evaluated beforehand through (auto)correlation analysis of variables. For the chosen pairs of AHC in the examined rivers, we estimated the correlation between water levels at a downstream AHC with different lead times and the levels at an upstream AHC with different time shift. In the case of the Pshish River, the correlation between the downstream AHC-95 and the upstream AHC-50 was highest―up to 0.93―at the lead time of 15–20 h ( Fig. 2a ). Similarly, the travel time, determined by the time of passage of appropriate high flood peaks in this reach, as mentioned above, is ~18 h. The autocorrelation at AHC-95 at an lead time up to 8 h, never falls below 0.95 and that at an lead time up to 13 h, below 0.90 ( Fig. 2b ). In the case of the Mzymta, because of the considerable changes in the drainage area between AHCs and a large lateral inflow, the correlation between the levels at the downstream AHC-160 and the upstream AHC-89 is not high ( Fig. 2c ): it is not greater than 0.74 for the lead time of 1 h and starts decreasing after 5 h. At active snow melting in the Mzymta R. catchment, the travel time of the wave of the daily level variation in the reach under consideration is 2–3.5 h. Conversely, the autocorrelation between the hourly levels of AHC-160 is relatively high: it is 0.97 below 1 h and 0.90 below 17 h ( Fig. 2d ). The obtained estimates correspond to the travel time between AHCs.
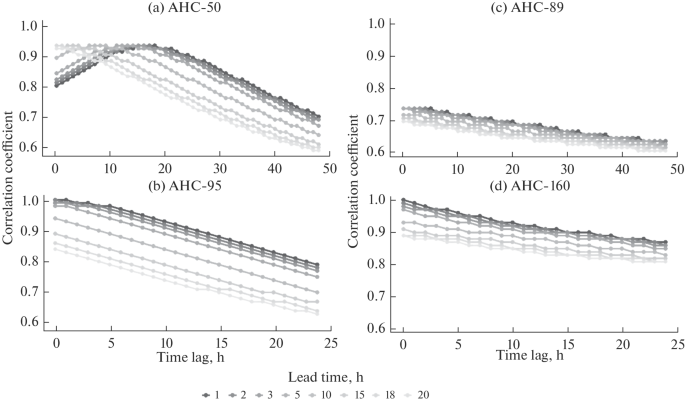
Corellogram of water levels in (a, b) the Pshish and (c, d) Mzymta rivers between the upstream and downstream gages and (b, d) autocorellogram at the downstream gage.
Grid search in the models’ hyperparameter space with ten-fold cross-validation on the training sample was used to determine optimal parameters and structures of the models and to evaluate modeling quality criteria with lead times of 1, 2, 3, 5, 10, 15, 18, and 20 h ( Table 2 ). The structure of the classification tree for model M5R became more complex with an increase in the lead time, though the interpretation of the chosen model configuration is available for any lead time in the form of a problem-solving graph (as, for example, in Fig. 3 for the lead time of 1 h). In the process of XGBoost model tuning, possible combinations of parameters were tested: the number of trees \( \in \) [100,300,500,800], the maximal depth of trees \(~ \in \) [ 3 , 5 , 8 ]. The best results were obtained with a model with 1000 trees with depth ≤5. In MLP model for the lead time of 5 h, a structure with one layer containing 10 neurons was used, while at another lead time, the structure is more complex―two or three layers each containing 10 neurons.
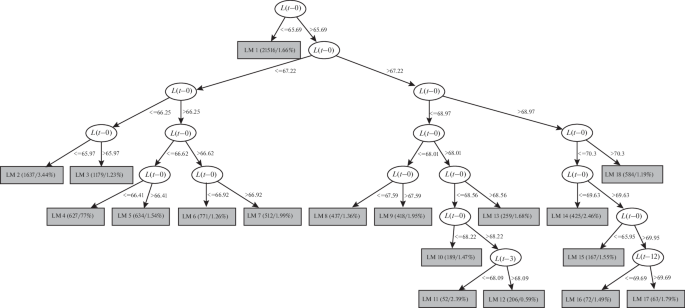
Decision tree of M5P model for water level forecast in the Pshish river at Guriiskaya Vil. at lead time of 1 h.
For the Pshish River, the best result in terms of NSE values was obtained for all models on the training and test samples with the lead times of 1–5 h. In the case of lead times less than 5 h, the root-mean-square error of simulation S ≤ 0.2 m. In the test period, the error S increases faster than in the calibration period and amounts to 0.25–0.41 m. As the lead time increases, the quality estimates in the form of NSE criterion steadily decrease, though remaining greater than 0.8, which corresponds to an excellent result of simulation. Tests based on independent data show that the best estimates were given by models M5P and XGBoost, in the latter case, with the lead time ≥10 h.
Estimates of the prognostic properties of simulation results by the S /σ Δ criterion show that the best forecast can be obtained at the lead times of 15 and 18 h, which is close to the travel time in the reach between the chosen gages AGK-95 and AGK-50 in the Pshish river and which is in agreement with the results of correlation analysis.
Simulation of individual flood events in the Pshish river was analyzed. Below, we discuss the simulation of the highest (historical) flood of October 24–26, 2018, with examples of lead time of 5 and 15 h ( Fig. 4 ).
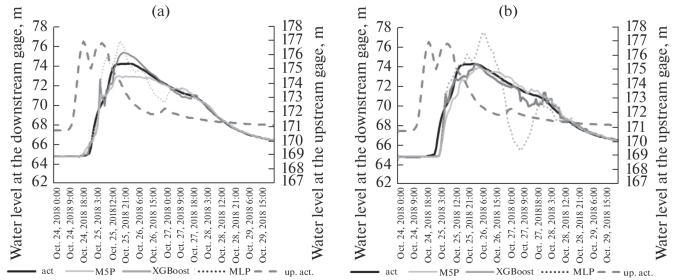
Actual and simulated plots of water level variations at the passage of flood of October 25–26, 2018, in the Pshish river. The lead time is 5 h in the left part and 15 h in the right part.
For the lead time of 5 and 15 h in the case of the flood of October 25, 2018, MLP model appreciably overestimates the maximal level―by 2.3–3.2 m, respectively. MLP model predicts earlier rise of the level to the marks of an adverse event (AE) (71.802 m) and a hazardous event (HE) (72.802 m) 5 h earlier than their actual time at the lead time of 5 and 4 h earlier than that at the lead time of 15 h. At the flood decay, MLP model demonstrates an abrupt drop in the level, which may be due to the interpretation by the model of a two-peak flood at the upper gage AHC-95, the levels of which are components of predictors for level forecasts at the lower gage AHC-50.
Some perturbation at the flood rise can be seen in the results of M5P model; however, this perturbation decays quickly. At the lead time of 5 h, M5P model overestimates peak floods by 1.1 m; at an lead time of 15 h, the model predicts level reaching AE mark 2 h earlier, but the forecasted time of HE mark is later and the level is 1.0–1.3 m lower than the observed values.
The results of simulation of the same flood by XGBoost model are less convincing, because the model predicts later times of AE and HE marks and underestimates the water levels by 1.0–1.7 m. In that case, at the lead time of 5 h, XGBoost model always underestimates peak water levels, and at the lead time of 15 h, its behavior is similar to that of M5P model, and its forecast of the time of HE level is 4 h later. Thus, the actual lead time in the forecast of HE mark time is 19 and 12–11 h by the models MLP and M5P, respectively.
Overall, the best results of simulation for the historical flood of October 24–25, 2018, on the Pshish river are obtained by two models: M5P and MLP. It is also worth mentioning that XGBoost shows smoother flood rises and falls, unlike MLP with its more abrupt response to changes in predictors. Models M5P and MLP at the forecast can overestimate the values of flood levels in the domain of the values not observed before. Notwithstanding the poorer result of MLP model, estimates NSE and S/ σ Δ show good prognostic qualities of the model in the case of an outstanding flood.
Similar tests of the models were made for the Mzymta river. The obtained results are given in Table 3 . Note that the efficiency of the models estimated by NSE , decays with each step at the lead time from 0.98 to 0.6 much faster than it does in the case of the Pshish river. This is due to the much shorter travel time between the upstream AHC-89 and downstream AHC-160, which is <4 h. In addition, at high floods, the peak forms earlier at the downstream gage because of the direction of motion of air masses from the coast toward mountains and the successive inclusion of parts of the catchment in the runoff formation and transformation processes, which reduces the role of levels at the upstream gage as predictors. The root-mean-square errors of simulation vary from 0.02 to 0.40 m over the training period and from 0.03 to 0.19 m over the test period.
All three models show an appreciable decrease in NSE efficiency over the test period, though most stable results in this case were obtained with the use of multilayer perceptron. The considerable decrease of the efficiency M5P and XGBoost models over the verification period can be attributed to overfitting.
In the case of the Mzymta river, the prognostic efficiency by criterion S /σ Δ is not met. Better simulation results were obtained for the lead times of 3 and 5 h. This demonstrates the need to incorporate additional hydrometeorological predictors for the development of more efficient prognostic procedures and for increasing the lead time. Similarly, the simulation of individual flood events was analyzed for the Mzymta river. The highest flood of October 25–26, 2018, included in the test period, is described by all models with underestimation of maximal water levels and a time lag relative to the observed values ( Fig. 5 ).
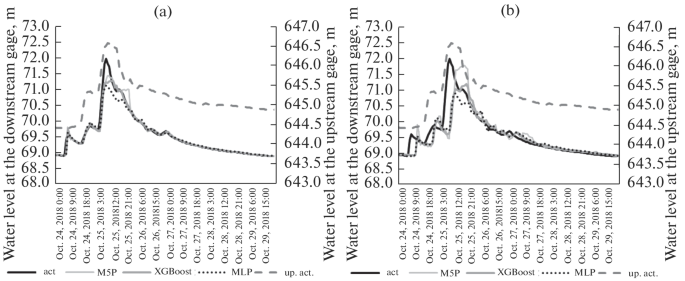
Actual and simulated plots of water level variations at the passage of flood of October 25, 2018, in the Mzymta river. The lead time is 1 h in the left part and 5 h in the right part.
The quality of water level simulations over the chosen period for the Pshish river is higher than that for the reach of the Mzymta river. The observed differences between simulation quality in the reaches of the Pshish and Mzymta can be attributed to differences between the natural conditions in their catchments. The area of the lateral part of the catchment is larger than that of the catchments for upstream gages (by factors of 1.3 and 1.9, respectively); however, the inflow has no considerable effect on the propagation of the flood wave in the Pshish river alone. The lateral catchment in the Pshish river reach from Navaginskoe Vil. to Guriiskaya st. has fairly smooth slope with elevations ≤700 m, and the processes in it appear to be synchronous with those in the upper catchment, where the runoff of high floods is mainly formed due to high rainfall. Downstream of Khadyzhensk town, additional inflow can be very low because of the small rainfall-runoff ratio in the lowland part of the catchment, and the character of the Pshish river becomes transit [ 8 ]. The large travel time in this reach is due to the small channel slope (with a drop from 180 to 80 m abs.).
Within the boundaries of the higher catchment of the Mzymta R., the processes of runoff formation and flood wave transformation in the examined reach are more complicated because of altitudinal zonation (which affect the proportions between the snowmelt and rain runoff) and a system of differently directed ridges, which affect moist air masses’ movement. The catchment of the Mzymta from its confluence with the Pslukh river to Kazachii Brod includes middle-mountain Krasnopolyanskaya depression (with elevations of 500–2000 m) and a low-mountain zone of the so-called pre-ascent of air masses (up to ~1000 m), open toward the Black Sea coast [ 10 ]. Here, the lateral inflow is a powerful factor that affects the variations of water level and hampers the development of level regime models taking into account only the upper gages (ANS-89) located in the upper reaches of the river. In addition, dredging and bank protection operations are carried out in the river channel even after the Winter Olympic Games 2014; these operations can have an effect on the level regime near the upstream gage. In the area near the downstream gage at Kazachii Brod, the level regime in some periods (e.g., October 17–28, 2019) shows the effects of releases from the Krasnopolyanskaya HPP with a range of variations up to 25 cm. The small travel time in this reach is due, in particular, to the large channel slope (with a drop from 650 to 70 m abs. in a reach half as long as that in the Pshish river).
In the Pshish river case study, which shows considerable correlation between water levels at the upper and lower AHC, the best results were obtained using decision trees boosting model, i.e., in essence, an ensemble of linear models, which most effectively utilizes the correlation within the sample. The complex nonlinear MLP model showed the worst results among the three models at each lead time, clearly, because of overfitting. However, its results can have a high prognostic potential for high floods, as it has been shown in the case of an extreme flood in October 2018. The effectiveness of the forecast is highest at the lead time of 15 and 18 h. Therefore, the results of simulation for the Pshish river, which simulate the patterns of flood wave transformation in a river reach, complement the results obtained by the method of corresponding levels (water discharges) for a larger river in the region, i.e., the Kuban [ 15 ], though with a one-hour instead of one-day step and with the use of state of the art technologies.
In the Mzymta river case study the relationship between the predictor and predictant is significantly weaker because of the substantial and asynchronous lateral inflow ( Fig. 2 ). The nonlinear model MLP was found to be best among the three models, which can be an indirect indication to its ability to detect additional relationships within the sample. And, although the simulation quality with an lead time up to 5 h is evaluated by NSE criterion as excellent, the stricter criterion of forecast efficiency S /σ Δ does not consider the results as satisfactory. Details of behavior of this criterion with an increase in lead time are discussed in [ 11 ]. More effective forecast models for water levels and/or discharges in the Mzymta river can be developed with the incorporation of additional data on the behavior of tributaries and meteorological data.
CONCLUSIONS
The study showed that machine learning methods applied to simulate water levels can give reliable forecasts. For the lower reaches of the Pshish river, the optimal lead time is 15–18 h. In the case of the Mzymta river at Kazachii Brod, with data on water levels at the upper gage at the confluence with the Pslukh river taken into account, the quality of simulation is estimated as good, though the required forecast efficiency has not been achieved. This is the effect of the considerable lateral inflow in the middle and lower reaches of the river and the asynchronous runoff formation in different parts of the catchment.
For the reach of the Pshish river, the best results of water level simulation were obtained with the use of the model of decision tree boosting (XGBoost), e.g., an ensemble of linear models, which most effectively use the correlation within the sample. Models M5P and MLP can successfully supplement and improve the forecasts in the case of high floods.
In the case of the Mzymta river, on the contrary, the best among the three models was the nonlinear MLP model, a fact, which may imply its ability to identify nonlinear relations within the dataset. Further studies will be focused on the search for interpretable neuron networks. This is currently a compelling research topic [ 26 , 44 ]. To improve the simulation quality of water level in the Mzymta River, it is reasonable to incorporate additional source data on water levels in tributaries and meteorological data.
Overall, the use of machine learning methods to construct procedures for forecasting floods in Krasnodar Krai rivers based on data of AMSFS KK network looks promising. The accumulation of long enough sets of precipitation data with an hourly step will enable studying the potential of artificial intelligence models in problems of rainfall-runoff forecasting and nowcasting.
Alekseevskii, N.I., Magritskii, D.V., Koltermann, P.K., Toropov, P.A., Shkol’nyi, D.I., and Belyakova, P.A., Inundations on the Black Sea Coast of Krasnodar Krai, Water Resour ., 2016, vol. 43, no. 1, pp. 1–14.
Article Google Scholar
Belyakova, P.A., Moreido, V.M., and P’yankova, A.I., Flood fatalities age and gender structure analysis in Russia in 2000−2014, Tret’i Vinogradovskie chteniya. Grani gidrologii (Third Vinogradov Conference. Facets of Hydrology), 2018, pp. 849–853.
Borsch, S.V., Simonov, Yu.A., and Khristoforov, A.V., Flood forecasting and early warning system for rivers of the Black Sea shore of Caucasian region and the Kuban river basin, Tr. Gidromettsentra RF , 2015, Special Issue 356.
Borsch, S.V. and Khristoforov, A.V., Hydrologic flow forecast verification, Tr. Gidromettsentra Rossii , 2015, Spec. Iss. 355.
Vasil’eva, E.S., Belyakova, P.A., Aleksyuk, A.I., Selezneva, N.V., and Belikov, V.V., Simulating flash floods in small rivers of the Northern Caucasus with the use of data of automated hydrometeorological network, Water Resour., 2021, vol. 48, no. 2, pp. 182–193.
Integrirovannoe upravlenie pavodkami. Kontseptual’nyi dokument VMO no. 1047 (Integrated Flood Management. Concept Paper. WMO-no.1047), Geneva, 2009.
Kuzin, P.S., Klassifikatsiya rek i gidrologicheskoe raionirovanie SSSR (Classification of Rivers and Hydrological Zoning of the USSR), Leningrad: Gidrometeoizdat, 1960.
Lur’e, P.M., Panov, V.D., and Tkachenko, Yu.Yu., Reka Kuban’. Gidrografiya i rezhim stoka (The Kuban River: Hydrography and Flow Regime), St. Petersburg: Gidrometeoizdat, 2005.
Nastavlenie po sluzhbe prognozov (Instruction on Forecast Service), Section 3, Pt. 1, Prognozy rezhima vod sushi (Forecasts of Continental Water Regime), Leningrad: Gidrometeoizdat, 1962.
Panov, V.D., Bazelyuk, A.A., and Lur’e, P.M., Reki Chernomorskogo Poberezh’ya Kavkaza: gidrografiya i rezhim stoka (Rivers of the Caucasian Black Sea Coast: Hydrography and Flow Regime), Rostov-on-Don.: Donskoi izd. dom, 2012.
Sokolov, A.A. and Bugaets, A.N., To the problem of verification of methods for short-range forecasting of hydrological parameters, Russ. Meteorol. Hydrol ., 2018, no. 8, pp. 539–543.
Tkachenko, Yu.Yu. and Sherzhukov, E.L., Experience in developing systems of short-term forecast of hydrological type of hazards, Vod. Khoz. Rossii: Probl., Tekhnol., Upravl., 2014, no. 3, pp. 75–82.
Sheverdyaev, I.V., Kleshchenkov, A.V., and Misirov, S.A., Flood hazard factors in rivers of the Northwestern Caucasus, Nauka Yuga Ross. , 2021, vol. 17, no. 1, pp. 37–51.
Google Scholar
Tsyplenkov, A.S., Ivanova, N.N., Botavin, D.V., Kuznetsova, Yu.S., and Golosov, V.N., Hydro-meteorological preconditions and geomorphological consequences of extreme flood in the small river basin in the wet subtropical zone (the Tsanyk River case study, Sochi region), Vestn. S.-Peterb. Univ., Nauki Zemle , 2021, vol. 66, no. 1, pp. 144–166.
Yumina, N.M. and Kuksina, L.V., Forecasted and calculated river discharge in the Kuban river basin, Vestn. Mosk. Univ., Ser. 5: Geogr ., 2011, no. 1, pp. 55–59.
Abrahart, R.J., Anctil, F., Coulibaly, P., Dawson, Ch.W., Mount, N.J., See, L.M., Shamseldin, A.Y., Solomatine, D.P., Toth, E., and Wilby, R.L., Two decades of anarchy? Emerging themes and outstanding challenges for neural network river forecasting, Progr. Phys. Geogr.: Earth Environ. , 2012, vol. 36, no. 4, pp. 480–513. https://doi.org/10.1177/0309133312444943
Beven, K., Deep learning, hydrological processes and the uniqueness of place, Hydrol. Processes , 2020, vol. 34, no. 16, pp. 3608–3613.
Bhattacharya, B. and Solomatine, D.P., Machine learning in sedimentation modelling, Neur. Networks , 2006, vol. 19, no. 2, pp. 208–214. https://doi.org/10.1016/j.neunet.2006.01.007
Brooks, K.N., Ffolliott, P.F., and Magner, J.A., Hydrology and the Management of Watersheds , 4th ed., Ames, Iowa: Wiley-Blackwell, 2013. https://doi.org/10.1002/9781118459751
Book Google Scholar
Chen, T. and Guestrin, C., XGBoost: A Scalable Tree Boosting System, Proc., 22nd ACM SIGKDD Int. Conf. Knowledge Discovery Data Mining , pp. 785–794. https://doi.org/10.1145/2939672.2939785
Chernokulsky, A.V., Kozlov, F.A., Zolina, O.G., Bulygina, O.N., Mokhov, I.I., and Semenov, V.A., Observed changes in convective and stratiform precipitation in Northern Eurasia over the last five decades, Environ. Res. Let ., 2019, vol. 4, no. 4, ACM SIGKDD Int. Conf. Knowledge Discovery Data Mining. P. 785–794. https://doi.org/10.1145/2939672.2939785
Emori, S. and Brown, S.J., Dynamic and thermodynamic changes in mean and extreme precipitation under changed climate, Geophys. Res. Lett ., 2005, vol. 32, p. L17706. https://doi.org/10.1029/2005GL023272
Ghahramani, Z., Probabilistic machine learning and artificial intelligence, Nature , 2015, vol. 521, pp. 452–459. https://doi.org/10.1038/nature14541
Haykin, S., Neural Networks and Learning Machines , 3rd ed. Upper Sadle River, New York: Prentice Hall Publ., 2009.
IPCC, 2013: Climate Change 2013: The Physical Science, Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, T.F. Stocker, D. Qin, G.-K. Plattner, M. Tignor, S.K. Allen, J. Boschung, A. Nauels, Y. Xia, V. Bex, and P.M. Midgey, Cambridge, United Kingdom; NY, USA: Cambridge Univ. Press,
Jain, A., Sudheer, K.P., and Srinivasulu, S., Identification of physical processes inherent in artificial neural network rainfall runoff models, Hydrol. Processes , 2004, vol. 18, no. 3, pp. 571–581.
Lehmann, J., Coumou, D., and Frieler, K., Increased record-breaking precipitation events under global warming, Clim. Change , 2015, no. 4, vol. 132, pp. 501–515.
Luo, J., Ying, K., and Bai, J., Savitzky-Golay smoothing and differentiation filter for even number data, Signal Process ., 2005, vol. 85, no. 7, pp. 1429–1434. https://doi.org/10.1016/j.sigpro.2005.02.002
Manual on Flood Forecasting and Warning , WMO, no. 1072, Geneva, 2011.
McCulloch, W.S. and Pitts, W., A logical calculus of the ideas immanent in nervous activity, Bull. Math. Biophys ., 1943, vol. 5, pp. 115–133. https://doi.org/10.1007/BF02478259
Moreido, V.M., Gartsman, B.I., Solomatine, D.P., and Suchilina, Z.A., Prospects for short-term forecasting of river streamflow from small watershed runoff using machine learning methods, Hydrosphere. Hazard Process. Phenom ., 2020, vol. 2, no. 4, pp. 375–390. https://doi.org/10.34753/HS.2020.2.4.375
Moreido, V., Gartsman, B., Solomatine, D.P., and Suchilina, Z., How well can machine learning models perform without hydrologists? Application of rational feature selection to improve hydrological forecasting, Water (Switzerland) , 2021, vol. 13, no. 12, p. 1696. https://doi.org/10.3390/w13121696
Mutlu, E., Chaubey, I., Hexmoor, H., and Bajwa, S.G., Comparison of artificial neural network models for hydrologic predictions at multiple gauging stations in an agricultural watershed, Hydrol. Process ., 2008, vol. 22, no. 26, pp. 5097–5106. https://doi.org/10.1002/hyp.7136
Nash, J.E. and Sutcliffe, J.V., River flow forecasting through conceptual models part I—A discussion of principles, J. Hydrol ., 1970, vol. 10, no. 3, pp. 282–290. https://doi.org/10.1016/0022-1694(70)90255-6
Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., Blondel, M., Prettenhofer, P., Weiss, R., Dubourg, V., Vanderplas, J., Passos, A., Cournapeau, D., Brucher, M., Perrot, M., and Duchesnay, E., Scikit-learn: Machine Learning in Python, J. Machine Learning Res ., 2011, vol. 12, pp. 2825–2830.
Press, W.H. and Teukolsky, S.A., Savitzky-Golay smoothing filters, Comput. Phys ., 1990, vol. 4, no. 6, p. 669. https://doi.org/10.1063/1.4822961
Quinlan, J.R., Learning with continuous classes, Proc. 5th Australian Joint Conf. Artificial Intelligence , 1992, pp. 343–348.
Reichstein, M., Camps-Valls, G., Stevens, B., Jung, M., Denzler, J., and Carvalhais, N., Prabhat, Deep learning and process understanding for data-driven Earth system science, Nature , 2019, vol. 566, pp. 195–204. https://doi.org/10.1038/s41586-019-0912-1
Rodda, H.J.E. and Little, M.A., Understanding Mathematical and Statistical Techniques in Hydrology , Chichester: UK: Wiley, 2015. https://doi.org/10.1002/9781119077985
Rolnick, D., Ahuja, A., Schwarz, J., Lillicrap, T.P., and Wayne, G., Experience replay for continual learning, Advances in Neural Information Processing Systems , 2018, vol. 32. http://arxiv.org/abs/1811.11682
Rumelhart, D.E., Hinton, G.E., and Williams, R.J., Learning representations by back-propagating errors, Nature , 1986, vol. 323, pp. 533–536. https://doi.org/10.1038/323533a0
Savitzky, A. and Golay, M.J.E., Smoothing and differentiation of data by simplified least squares procedures, Anal. Chem ., 1964, vol. 36, no. 8, pp. 1627–1639. https://doi.org/10.1021/ac60214a047
Senthil Kumar, A.R., Sudheer, K.P., Jain, S.K., and Agarwal, P.K., Rainfall-runoff modelling using artificial neural networks: comparison of network types, Hydrol. Processes , 2005, vol. 19, no. 6, pp. 1277–1291. https://doi.org/10.1002/hyp.5581
Shen, C.A., Transdisciplinary review of deep learning research and its relevance for water resources scientists, Water Resour. Res ., 2018, vol. 54, no. 11, pp. 8558–8593.
Sylvester, Z., Durkin, P., Covault, J.A., and Sharman, G.R., High curvatures drive river meandering: REPLY, Geol ., 2019, vol. 47, no. 10. P. e486–e486. https://doi.org/10.1130/G46838Y.1
WMO, 2012. Management of Flash Floods, Integrated Flood Management Tools Series , no. 16, Geneva, 2012.
Download references
Data processing and modeling were supported by the Russian Science Foundation and Krasnodar krai under research project 19-45-233007; DEM was processed under RFBR Project 19-05-00353; the interpretation of results was carried out under subject 147-2019-0001 (state registration AAAA-A18-118022090056-0) of the State Assignment to Water Problems Institute, Russian Academy of Sciences. A.S. Tsyplenkov was supported by the Development Program of the Interdisciplinary Scientific-Educational School at Moscow State University “The Future of the Planet and Global Environmental Changes”).
Author information
Authors and affiliations.
Water Problems Institute, Russian Academy of Sciences, 119333, Moscow, Russia
P. A. Belyakova, V. M. Moreido & A. N. Amerbaev
Pacific Geographical Institute, Far Eastern Branch, Russian Academy of Sciences, 690041, Vladivostok, Russia
P. A. Belyakova
Moscow State University, 119991, Moscow, Russia
A. S. Tsyplenkov & D. A. Grechishnikova
State Hydrological Institute, 199004, St. Petersburg, Russia
L. S. Kurochkina
Special Center for Hydrometeorology and Environmental Monitoring for the Black Sea and the Sea of Azov, 354057, Sochi, Russia
V. A. Filippov
OOO Emersit, 350001, Krasnodar, Russia
M. S. Makeev
You can also search for this author in PubMed Google Scholar
Corresponding author
Correspondence to P. A. Belyakova .
Rights and permissions
Open Access. This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .
Reprints and permissions
About this article
Belyakova, P.A., Moreido, V.M., Tsyplenkov, A.S. et al. Forecasting Water Levels in Krasnodar Krai Rivers with the Use of Machine Learning. Water Resour 49 , 10–22 (2022). https://doi.org/10.1134/S0097807822010043
Download citation
Received : 16 August 2021
Revised : 17 August 2021
Accepted : 18 August 2021
Published : 05 March 2022
Issue Date : February 2022
DOI : https://doi.org/10.1134/S0097807822010043
Share this article
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- hydrological forecasts
- machine learning
- artificial neural networks
- flash floods
- short-term water level forecasts
- Find a journal
- Publish with us
- Track your research
- You are on Realigro website
- Russian Federation
Krasnodar Krai
- List your properties
- Estate agents
- Private seller
- Property portals
Preferences
- Publish your free listing
- Rent-holidays
Listings houses for sale, Krasnodar Krai
Listings for sale.
- Save search
- Submit a generic request
- Custom search

Real Estate Listings
For sale farmland, russian federation, krasnodar krai, sapozhok, sapozhkovskyi rayon.

Refine your search
Search by area.
- Sapozhok (1)
Search by category
- Beach Resort (1)
- Farmland (1)
For a better use of Realigro website, set your preferences for language, currency, square meters or sq ft.
InfoQ Software Architects' Newsletter
A monthly overview of things you need to know as an architect or aspiring architect.
View an example
We protect your privacy.
QCon San Francisco (Nov 18-22): Get assurance you’re adopting the right software practices. Register Now
Facilitating the Spread of Knowledge and Innovation in Professional Software Development
- English edition
- Chinese edition
- Japanese edition
- French edition
Back to login
Login with:
Don't have an infoq account, helpful links.
- About InfoQ
- InfoQ Editors
Write for InfoQ
- About C4Media
Choose your language
Get clarity from senior software practitioners on today's critical dev priorities. Register Now.
Level up your software skills by uncovering the emerging trends you should focus on. Register now.
Discover emerging trends, insights, and real-world best practices in software development & tech leadership. Join now.
Your monthly guide to all the topics, technologies and techniques that every professional needs to know about. Subscribe for free.
InfoQ Homepage News JSpecify 1.0.0 and Nullability in Java
JSpecify 1.0.0 and Nullability in Java
Aug 12, 2024 6 min read
The JSpecify collective has made their first release, JSpecify 1.0.0. The group's mission is to define common sets of annotation types for use in JVM languages, to improve static analysis and language interoperation.
The projects and groups in the consensus include:
- Android, Error Prone, Guava (Google)
- Kotlin, IntelliJ (JetBrains)
- Azure SDK (Microsoft)
By participating in JSpecify, the members guarantee their projects will be backwards compatibility at source level. This means that they will not rename the annotations in the jar, move them or make other changes that would cause code compilation to fail due to an update. In other words, it is safe to depend on it, and it won't be changed in any way that breaks application code.
This initial release focuses on the use of type-use annotations to indicate the nullability status of usages of static types. The primary use cases are expected to be variables, parameters and return values, but they can be used anywhere that tracking nullness makes conceptual sense.
Some possibilities do not pass the "conceptual sense" test however - e.g. you still can't write things like class Foo extends @Nullable Bar .
Background on nullability and nullness checkers
The subject of nullability has long been a topic of debate in the Java ecosystem. The idea is that developers should be better insulated from NPEs, as large swathes of use cases that currently could cause NPEs will be ruled out at build time.
However, this promising idea has been held up by some unfortunate facts, specifically that Java has both:
- A long history which largely predates viable concepts of non-nullable values in programming languages.
- A strong tradition of backwards compatability.
It has therefore been difficult to see a path forward that allows null-awareness to be added to the language in a consistent and non-breaking fashion.
Nevertheless, attempts have been made -- the most famous is probably JSR 305 which ran for several years, but eventually became Dormant in 2012 without being completed and fully standardized.
After the failure of that effort, various companies and projects pressed ahead with their own versions of nullability annotations. Some of these projects were trying to solve primarily for their own use cases, but others are intended to be broadly usable by Java applications.
Of particular interest is the Kotlin language, which has built null-awareness into the type system. This is achieved by assuming that, for example, String indicates a value that cannot be null , and requiring the developer to explicitly indicate nullability as String? . This is mostly very successful, at least as long as a program is written in pure Kotlin.
Java developers sometimes exclaim that they "just want what Kotlin has", but as the Kotlin docs make clear there are a number of subtleties here, especially when interoperating with Java code.
Currently, in the pure Java space, most current projects approach nullability by treating the null status as extra information to be processed via a build-time checker (static analysis) tool. By adding additional information in the form of annotations, then the checker aims to reduce or eliminate NPEs from the program the analysis was run on.
Different projects have different philosophies about how much of a "soundness guarantee" they want to offer. Soundness comes at a cost - more complexity, more effort to migrate your codebase, more false positives to deal with, so not every developer will want full and complete guarantees.
JSpecify represents an attempt to unify these approaches, and the initial goals are quite modest - version 1.0.0 defines only four annotations:
- @NullMarked
- @NullUnmarked
The first two can be applied to specific type usage (e.g. parameter definition or method return values), while the second pair can be broadly applied. Together, they provide usable declarative, use-site null-awareness for Java types.
One general common use case is to add @NullMarked to module, package or type declarations that you're adding nullability information to. This can save a lot of work, as it indicates that any remaining unannotated type usages are not nullable. Then, any exceptional cases can be explicitly marked as @Nullable - and this arrangement is the sensible choice for a default.
The intent is for end users to adopt (or continue to use) one of the participating projects - and different projects have different levels of maturity. For example, IntelliJ supports JSpecify annotations, but generics are still not fully supported yet.
A reference checker is also available , but this is not really intended for use by application developers, but instead is aimed at the projects participating in JSpecify.
There is also a FAQ covering the deeper, more technical aspects of the design .
InfoQ contacted one of the key developers working on JSpecify - Juergen Hoeller (Spring Framework project lead).
InfoQ: Please tell us about your involvement in JSpecify and nullability:
Hoeller: Together with Sebastien Deleuze, I've been working on the nullability design in Spring Framework 5 which led to our participation in JSpecify.
InfoQ: Can you explain how JSpecify is used in your projects and why it's important to them?
Hoeller: The Spring Framework project and many parts of the wider Spring portfolio have adopted a non-null-by-default design in 2017, motivated by our Kotlin integration but also providing significant benefits in Java-based projects (in combination with IntelliJ IDEA and tools like NullAway). This is exposed in our public API for application-level callers to reason about the nullability of parameters and return values. It also goes deep into our internal codebase, verifying that our nullability assumptions and assertions match the actual code flow. This is hugely beneficial for our own internal design and maintenance as well. The original JSR 305 annotations were embraced quite widely in tools, despite never officially having been finished. Spring's own annotations use JSR 305 as meta-annotations for tool discoverability, leading to immediate support in IntelliJ IDEA and Kotlin. Our involvement in JSpecify started from that existing arrangement of ours since we were never happy with the state of the JSR 305 annotations and wanted to have a strategic path for annotation semantics and tool support going forward, allowing us to evolve our APIs and codebase with tight null safety.
InfoQ: It's taken 6 years to get to 1.0.0. Why do you think that it's taken so long?
Hoeller: While our current use cases in Spring are pretty straightforward, focusing on parameter and return values as well as field values, the problem space itself is complex overall. The JSpecify mission aimed for generics support which turned out to be rather involved. JSpecify 1.0 considers many requirements from many stakeholders, and it is not easy to reach consensus with such a wide-ranging collaborative effort.
InfoQ: What does the future look like, if JSpecify is successful?
Hoeller: For a start, JSpecify is well-positioned to supersede JSR 305 for tool support and for common annotations in open source frameworks and libraries. It is critical to have such support on top of the currently common baselines such as JDK 17 since large parts of the open source ecosystem will remain on such a baseline for many years to come. Even on newer Java and Kotlin versions over the next few years, JDK 17 based frameworks and libraries will still be in widespread use, and JSpecify can evolve along with their needs.
InfoQ: What's next for JSpecify to tackle?
Hoeller: From the Spring side, we need official meta-annotation support so that we can declare our own nullability annotations with JSpecify meta-annotations instead of JSR 305 meta-annotations.
InfoQ: Thank you!
About the Author
Rate this article, this content is in the java topic, related topics:.
- Development
- Architecture & Design
- Culture & Methods
- Architecture
- Software Engineering
Related Editorial
Related sponsored content, [ebook] api security for the modern enterprise, related sponsor.
/filters:no_upscale()/sponsorship/topic/ab4e0ce7-864a-4131-b009-638fe135de28/CurityLogoRSB-1712304212846.png)
Protect Identities. Secure Digital Services. Enable scalable and secure user access to web and mobile applications. Start free trial .
Related Content
The infoq newsletter.
A round-up of last week’s content on InfoQ sent out every Tuesday. Join a community of over 250,000 senior developers. View an example

IMAGES
COMMENTS
Null Hypothesis H 0: Group proportions are equal in the population: p 1 = p 2. Alternative Hypothesis H A: ... In the case of a one-sided hypothesis test, the null still contains an equal sign but it's "greater than or equal to" or "less than or equal to." If you wanted to translate the null hypothesis from its native mathematical ...
Research question: Null hypothesis (H 0): General: Test-specific: Does tooth flossing affect the number of cavities? Tooth flossing has no effect on the number of cavities.: t test:. The mean number of cavities per person does not differ between the flossing group (µ 1) and the non-flossing group (µ 2) in the population; µ 1 = µ 2.: Does the amount of text highlighted in the textbook ...
H A: At least one group mean is different from the rest; To decide if we should reject or fail to reject the null hypothesis, we must refer to the p-value in the output of the ANOVA table. If the p-value is less than some significance level (e.g. 0.05) then we can reject the null hypothesis and conclude that not all group means are equal.
Example 1: Weight of Turtles. A biologist wants to test whether or not the true mean weight of a certain species of turtles is 300 pounds. To test this, he goes out and measures the weight of a random sample of 40 turtles. Here is how to write the null and alternative hypotheses for this scenario: H0: μ = 300 (the true mean weight is equal to ...
The null hypothesis and the alternative hypothesis are types of conjectures used in statistical tests to make statistical inferences, which are formal methods of reaching conclusions and separating scientific claims from statistical noise.. The statement being tested in a test of statistical significance is called the null hypothesis. The test of significance is designed to assess the strength ...
A null hypothesis is a statistical concept suggesting no significant difference or relationship between measured variables. It's the default assumption unless empirical evidence proves otherwise. The null hypothesis states no relationship exists between the two variables being studied (i.e., one variable does not affect the other).
The actual test begins by considering two hypotheses.They are called the null hypothesis and the alternative hypothesis.These hypotheses contain opposing viewpoints. H 0, the —null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.
It is the opposite of your research hypothesis. The alternative hypothesis--that is, the research hypothesis--is the idea, phenomenon, observation that you want to prove. If you suspect that girls take longer to get ready for school than boys, then: Alternative: girls time > boys time. Null: girls time <= boys time.
Review. In a hypothesis test, sample data is evaluated in order to arrive at a decision about some type of claim.If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we: Evaluate the null hypothesis, typically denoted with \(H_{0}\).The null is not rejected unless the hypothesis test shows otherwise.
This null hypothesis can be written as: H0: X¯ = μ H 0: X ¯ = μ. For most of this textbook, the null hypothesis is that the means of the two groups are similar. Much later, the null hypothesis will be that there is no relationship between the two groups. Either way, remember that a null hypothesis is always saying that nothing is different.
10.1 - Setting the Hypotheses: Examples. A significance test examines whether the null hypothesis provides a plausible explanation of the data. The null hypothesis itself does not involve the data. It is a statement about a parameter (a numerical characteristic of the population). These population values might be proportions or means or ...
A null hypothesis is a statement that there is no difference between two groups or that there is no association between two variables. In other words, the null hypothesis assumes that any observed differences are due to chance. ... You would give the pill to one group of people and not give it to another group (the control group). If the people ...
β 1: The average change in y associated with a one unit increase in x. x: The value of the predictor variable. Simple linear regression uses the following null and alternative hypotheses: H 0: β 1 = 0; H A: β 1 ≠ 0; The null hypothesis states that the coefficient β 1 is equal to zero. In other words, there is no statistically significant ...
The most common null hypothesis test for this type of statistical relationship is the t test. In this section, we look at three types of t tests that are used for slightly different research designs: the one-sample t test, the dependent-samples t test, and the independent-samples t test. The one-sample t test is used to compare a sample mean ...
Null Hypothesis Examples. "Hyperactivity is unrelated to eating sugar " is an example of a null hypothesis. If the hypothesis is tested and found to be false, using statistics, then a connection between hyperactivity and sugar ingestion may be indicated. A significance test is the most common statistical test used to establish confidence in a ...
Here, the hypothesis test formulas are given below for reference. The formula for the null hypothesis is: H 0 : p = p 0. The formula for the alternative hypothesis is: H a = p >p 0, < p 0 ≠ p 0. The formula for the test static is: Remember that, p 0 is the null hypothesis and p - hat is the sample proportion.
Null Hypothesis: A null hypothesis is a type of hypothesis used in statistics that proposes that no statistical significance exists in a set of given observations. The null hypothesis attempts to ...
A hypothesis test is a formal statistical test we use to reject or fail to reject a statistical hypothesis. We always use the following steps to perform a hypothesis test: Step 1: State the null and alternative hypotheses. The null hypothesis, denoted as H0, is the hypothesis that the sample data occurs purely from chance.
Krasnodar Krai is located in the southwestern part of the North Caucasus and borders Rostov Oblast in the northeast, Stavropol Krai and Karachay-Cherkessia in the east, and with the Abkhazia region (internationally recognized as part of Georgia) in the south. [14] The Republic of Adygea is completely encircled by the krai territory. The krai's Taman Peninsula is situated between the Sea of ...
Chushka (rural locality) / 45.33056°N 36.66667°E / 45.33056; 36.66667. Chushka ( Russian: Чушка́) is an abandoned village on the Chushka Spit in Zaporozhskoye Rural Settlement of Temryuksky District, in Krasnodar Krai, Russia. It is located beside Port Kavkaz, which includes the Kerch Strait ferry terminal, near the end of the spit.
Abstract The potential of construction of machine learning models was considered as applied to water level forecasting in mountain river reaches in Krasnodar Krai based on observation data on water levels at automated hydrological complexes of the Automated System of Flood Conditions Monitoring in Krasnodar Krai. The study objects were two mountain rivers in Krasnodar Krai―the Pshish and ...
390,060.00USD. For sale. Farmland. 7000000 m². Agricultural land for sale. Location- Russian Federation, Ryazanskaya region, Sapozhkovskyi district. The whole area is 700 hectares. The land is pri... Ask info about similar real estates.
Fortunately, a one sample t-test allows us to answer this question. One Sample t-test: Formula. A one-sample t-test always uses the following null hypothesis: H 0: μ = μ 0 (population mean is equal to some hypothesized value μ 0) The alternative hypothesis can be either two-tailed, left-tailed, or right-tailed:
The group's mission is to define common sets of annotation types for use in JVM languages, to improve static analysis and language interoperation. ... use-site null-awareness for Java types. One ...