examples of null hypothesis and alternative

Have a thesis expert improve your writing

Check your thesis for plagiarism in 10 minutes, generate your apa citations for free.

• Knowledge Base
• Null and Alternative Hypotheses | Definitions & Examples

Null and Alternative Hypotheses | Definitions & Examples

Published on 5 October 2022 by Shaun Turney . Revised on 6 December 2022.

The null and alternative hypotheses are two competing claims that researchers weigh evidence for and against using a statistical test :

• Null hypothesis (H 0 ): There’s no effect in the population .
• Alternative hypothesis (H A ): There’s an effect in the population.

The effect is usually the effect of the independent variable on the dependent variable .

Table of contents

Answering your research question with hypotheses, what is a null hypothesis, what is an alternative hypothesis, differences between null and alternative hypotheses, how to write null and alternative hypotheses, frequently asked questions about null and alternative hypotheses.

The null and alternative hypotheses offer competing answers to your research question . When the research question asks “Does the independent variable affect the dependent variable?”, the null hypothesis (H 0 ) answers “No, there’s no effect in the population.” On the other hand, the alternative hypothesis (H A ) answers “Yes, there is an effect in the population.”

The null and alternative are always claims about the population. That’s because the goal of hypothesis testing is to make inferences about a population based on a sample . Often, we infer whether there’s an effect in the population by looking at differences between groups or relationships between variables in the sample.

You can use a statistical test to decide whether the evidence favors the null or alternative hypothesis. Each type of statistical test comes with a specific way of phrasing the null and alternative hypothesis. However, the hypotheses can also be phrased in a general way that applies to any test.

The null hypothesis is the claim that there’s no effect in the population.

If the sample provides enough evidence against the claim that there’s no effect in the population ( p ≤ α), then we can reject the null hypothesis . Otherwise, we fail to reject the null hypothesis.

Although “fail to reject” may sound awkward, it’s the only wording that statisticians accept. Be careful not to say you “prove” or “accept” the null hypothesis.

Null hypotheses often include phrases such as “no effect”, “no difference”, or “no relationship”. When written in mathematical terms, they always include an equality (usually =, but sometimes ≥ or ≤).

Examples of null hypotheses

The table below gives examples of research questions and null hypotheses. There’s always more than one way to answer a research question, but these null hypotheses can help you get started.

*Note that some researchers prefer to always write the null hypothesis in terms of “no effect” and “=”. It would be fine to say that daily meditation has no effect on the incidence of depression and p 1 = p 2 .

The alternative hypothesis (H A ) is the other answer to your research question . It claims that there’s an effect in the population.

Often, your alternative hypothesis is the same as your research hypothesis. In other words, it’s the claim that you expect or hope will be true.

The alternative hypothesis is the complement to the null hypothesis. Null and alternative hypotheses are exhaustive, meaning that together they cover every possible outcome. They are also mutually exclusive, meaning that only one can be true at a time.

Alternative hypotheses often include phrases such as “an effect”, “a difference”, or “a relationship”. When alternative hypotheses are written in mathematical terms, they always include an inequality (usually ≠, but sometimes > or <). As with null hypotheses, there are many acceptable ways to phrase an alternative hypothesis.

Examples of alternative hypotheses

The table below gives examples of research questions and alternative hypotheses to help you get started with formulating your own.

Null and alternative hypotheses are similar in some ways:

• They’re both answers to the research question
• They both make claims about the population
• They’re both evaluated by statistical tests.

However, there are important differences between the two types of hypotheses, summarized in the following table.

To help you write your hypotheses, you can use the template sentences below. If you know which statistical test you’re going to use, you can use the test-specific template sentences. Otherwise, you can use the general template sentences.

The only thing you need to know to use these general template sentences are your dependent and independent variables. To write your research question, null hypothesis, and alternative hypothesis, fill in the following sentences with your variables:

Does independent variable affect dependent variable ?

• Null hypothesis (H 0 ): Independent variable does not affect dependent variable .
• Alternative hypothesis (H A ): Independent variable affects dependent variable .

Test-specific

Once you know the statistical test you’ll be using, you can write your hypotheses in a more precise and mathematical way specific to the test you chose. The table below provides template sentences for common statistical tests.

Note: The template sentences above assume that you’re performing one-tailed tests . One-tailed tests are appropriate for most studies.

The null hypothesis is often abbreviated as H 0 . When the null hypothesis is written using mathematical symbols, it always includes an equality symbol (usually =, but sometimes ≥ or ≤).

The alternative hypothesis is often abbreviated as H a or H 1 . When the alternative hypothesis is written using mathematical symbols, it always includes an inequality symbol (usually ≠, but sometimes < or >).

A research hypothesis is your proposed answer to your research question. The research hypothesis usually includes an explanation (‘ x affects y because …’).

A statistical hypothesis, on the other hand, is a mathematical statement about a population parameter. Statistical hypotheses always come in pairs: the null and alternative hypotheses. In a well-designed study , the statistical hypotheses correspond logically to the research hypothesis.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the ‘Cite this Scribbr article’ button to automatically add the citation to our free Reference Generator.

Turney, S. (2022, December 06). Null and Alternative Hypotheses | Definitions & Examples. Scribbr. Retrieved 4 November 2024, from https://www.scribbr.co.uk/stats/null-and-alternative-hypothesis/

Is this article helpful?

Shaun Turney

Other students also liked, levels of measurement: nominal, ordinal, interval, ratio, the standard normal distribution | calculator, examples & uses, types of variables in research | definitions & examples.

9.1 Null and Alternative Hypotheses

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 , the — null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.

H a —, the alternative hypothesis: a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are reject H 0 if the sample information favors the alternative hypothesis or do not reject H 0 or decline to reject H 0 if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in H 0 and H a :

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

Example 9.1

H 0 : No more than 30 percent of the registered voters in Santa Clara County voted in the primary election. p ≤ 30 H a : More than 30 percent of the registered voters in Santa Clara County voted in the primary election. p > 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25 percent. State the null and alternative hypotheses.

Example 9.2

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are the following: H 0 : μ = 2.0 H a : μ ≠ 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ __ 66
• H a : μ __ 66

Example 9.3

We want to test if college students take fewer than five years to graduate from college, on the average. The null and alternative hypotheses are the following: H 0 : μ ≥ 5 H a : μ < 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ __ 45
• H a : μ __ 45

Example 9.4

An article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third of the students pass. The same article stated that 6.6 percent of U.S. students take advanced placement exams and 4.4 percent pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6 percent. State the null and alternative hypotheses. H 0 : p ≤ 0.066 H a : p > 0.066

On a state driver’s test, about 40 percent pass the test on the first try. We want to test if more than 40 percent pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : p __ 0.40
• H a : p __ 0.40

Collaborative Exercise

Bring to class a newspaper, some news magazines, and some internet articles. In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-statistics . Changes were made to the original material, including updates to art, structure, and other content updates.

Access for free at https://openstax.org/books/statistics/pages/1-introduction

• Authors: Barbara Illowsky, Susan Dean
• Publisher/website: OpenStax
• Book title: Statistics
• Publication date: Mar 27, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/statistics/pages/1-introduction
• Section URL: https://openstax.org/books/statistics/pages/9-1-null-and-alternative-hypotheses

© Apr 16, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• Science, Tech, Math ›
• Statistics ›
• Inferential Statistics ›

Null Hypothesis and Alternative Hypothesis

• Inferential Statistics
• Statistics Tutorials
• Probability & Games
• Descriptive Statistics
• Applications Of Statistics
• Math Tutorials
• Pre Algebra & Algebra
• Exponential Decay
• Worksheets By Grade
• Ph.D., Mathematics, Purdue University
• M.S., Mathematics, Purdue University
• B.A., Mathematics, Physics, and Chemistry, Anderson University

Hypothesis testing involves the careful construction of two statements: the null hypothesis and the alternative hypothesis. These hypotheses can look very similar but are actually different.

How do we know which hypothesis is the null and which one is the alternative? We will see that there are a few ways to tell the difference.

The Null Hypothesis

The null hypothesis reflects that there will be no observed effect in our experiment. In a mathematical formulation of the null hypothesis, there will typically be an equal sign. This hypothesis is denoted by H 0 .

The null hypothesis is what we attempt to find evidence against in our hypothesis test. We hope to obtain a small enough p-value that it is lower than our level of significance alpha and we are justified in rejecting the null hypothesis. If our p-value is greater than alpha, then we fail to reject the null hypothesis.

If the null hypothesis is not rejected, then we must be careful to say what this means. The thinking on this is similar to a legal verdict. Just because a person has been declared "not guilty", it does not mean that he is innocent. In the same way, just because we failed to reject a null hypothesis it does not mean that the statement is true.

For example, we may want to investigate the claim that despite what convention has told us, the mean adult body temperature is not the accepted value of 98.6 degrees Fahrenheit . The null hypothesis for an experiment to investigate this is “The mean adult body temperature for healthy individuals is 98.6 degrees Fahrenheit.” If we fail to reject the null hypothesis, then our working hypothesis remains that the average adult who is healthy has a temperature of 98.6 degrees. We do not prove that this is true.

If we are studying a new treatment, the null hypothesis is that our treatment will not change our subjects in any meaningful way. In other words, the treatment will not produce any effect in our subjects.

The Alternative Hypothesis

The alternative or experimental hypothesis reflects that there will be an observed effect for our experiment. In a mathematical formulation of the alternative hypothesis, there will typically be an inequality, or not equal to symbol. This hypothesis is denoted by either H a or by H 1 .

The alternative hypothesis is what we are attempting to demonstrate in an indirect way by the use of our hypothesis test. If the null hypothesis is rejected, then we accept the alternative hypothesis. If the null hypothesis is not rejected, then we do not accept the alternative hypothesis. Going back to the above example of mean human body temperature, the alternative hypothesis is “The average adult human body temperature is not 98.6 degrees Fahrenheit.”

If we are studying a new treatment, then the alternative hypothesis is that our treatment does, in fact, change our subjects in a meaningful and measurable way.

The following set of negations may help when you are forming your null and alternative hypotheses. Most technical papers rely on just the first formulation, even though you may see some of the others in a statistics textbook.

• Null hypothesis: “ x is equal to y .” Alternative hypothesis “ x is not equal to y .”
• Null hypothesis: “ x is at least y .” Alternative hypothesis “ x is less than y .”
• Null hypothesis: “ x is at most y .” Alternative hypothesis “ x is greater than y .”
• What 'Fail to Reject' Means in a Hypothesis Test
• Type I and Type II Errors in Statistics
• An Example of a Hypothesis Test
• The Runs Test for Random Sequences
• An Example of Chi-Square Test for a Multinomial Experiment
• The Difference Between Type I and Type II Errors in Hypothesis Testing
• What Level of Alpha Determines Statistical Significance?
• What Is the Difference Between Alpha and P-Values?
• What Is ANOVA?
• How to Find Critical Values with a Chi-Square Table
• Example of a Permutation Test
• Degrees of Freedom for Independence of Variables in Two-Way Table
• Example of an ANOVA Calculation
• How to Find Degrees of Freedom in Statistics
• How to Construct a Confidence Interval for a Population Proportion
• Degrees of Freedom in Statistics and Mathematics

Hypothesis Testing: Null Hypothesis and Alternative Hypothesis

Join over 2 million students who advanced their careers with 365 Data Science. Learn from instructors who have worked at Meta, Spotify, Google, IKEA, Netflix, and Coca-Cola and master Python, SQL, Excel, machine learning, data analysis, AI fundamentals, and more.

Figuring out exactly what the null hypothesis and the alternative hypotheses are is not a walk in the park. Hypothesis testing is based on the knowledge that you can acquire by going over what we have previously covered about statistics in our blog.

So, if you don’t want to have a hard time keeping up, make sure you have read all the tutorials about confidence intervals , distributions , z-tables and t-tables .

We've also made a video on null hypothesis vs alternative hypothesis - you can watch it below or just scroll down if you prefer reading.

Confidence intervals provide us with an estimation of where the parameters are located. You can obtain them with our confidence interval calculator and learn more about them in the related article.

However, when we are making a decision, we need a yes or no answer. The correct approach, in this case, is to use a test .

Here we will start learning about one of the fundamental tasks in statistics - hypothesis testing !

The Hypothesis Testing Process

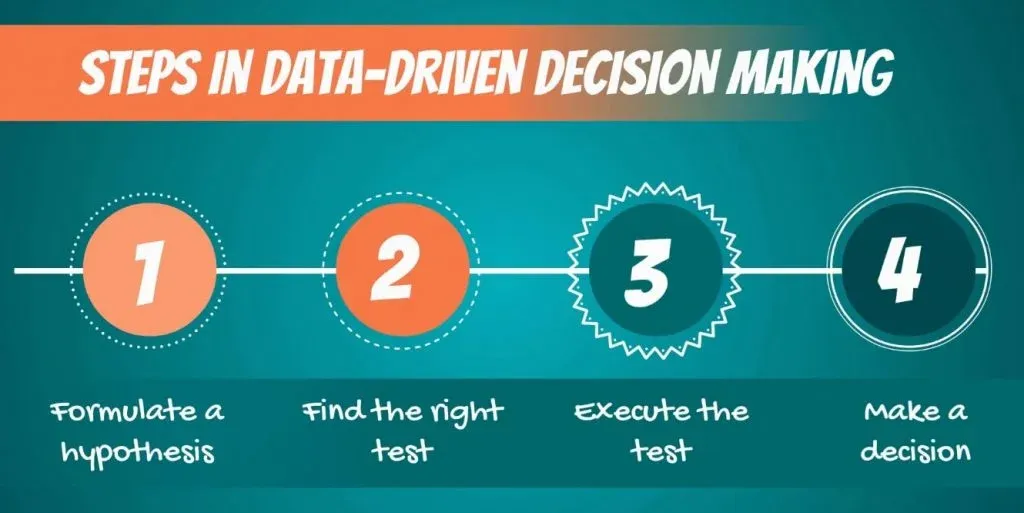
  First off, let’s talk about data-driven decision-making. It consists of the following steps:

• First, we must formulate a hypothesis .
• After doing that, we have to find the right test for our hypothesis .
• Then, we execute the test.
• Finally, we make a decision based on the result.

Let’s start from the beginning.

What is a Hypothesis?

Though there are many ways to define it, the most intuitive must be:

“A hypothesis is an idea that can be tested.”

This is not the formal definition, but it explains the point very well.

So, if we say that apples in New York are expensive, this is an idea or a statement. However, it is not testable, until we have something to compare it with.

For instance, if we define expensive as: any price higher than $1.75 dollars per pound, then it immediately becomes a hypothesis .

What Cannot Be a Hypothesis?

An example may be: would the USA do better or worse under a Clinton administration, compared to a Trump administration? Statistically speaking, this is an idea , but there is no data to test it. Therefore, it cannot be a hypothesis of a statistical test.

Actually, it is more likely to be a topic of another discipline.

Conversely, in statistics, we may compare different US presidencies that have already been completed. For example, the Obama administration and the Bush administration, as we have data on both.

A Two-Sided Test

Alright, let’s get out of politics and get into hypotheses . Here’s a simple topic that CAN be tested.

According to Glassdoor (the popular salary information website), the mean data scientist salary in the US is 113,000 dollars.

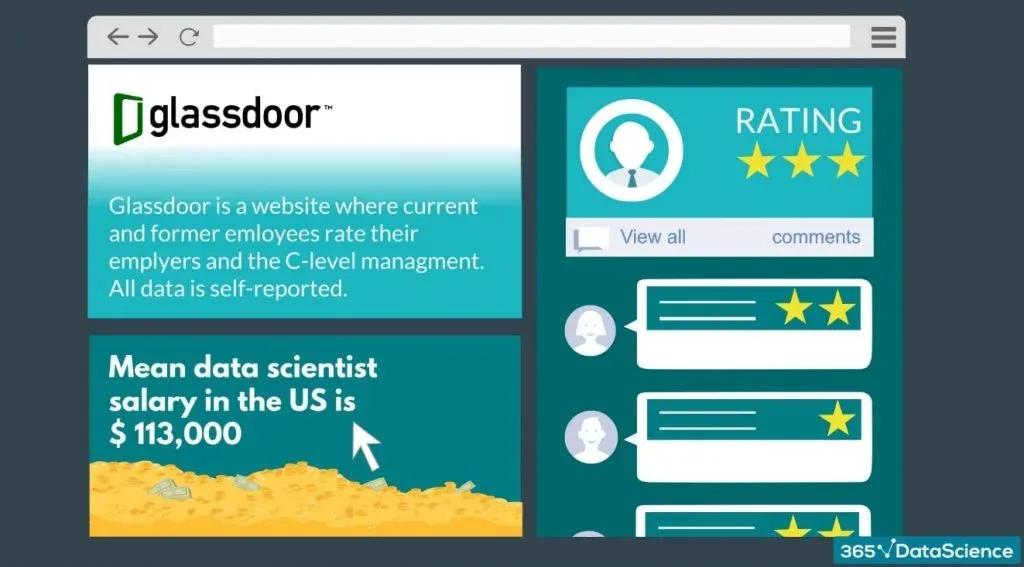
So, we want to test if their estimate is correct.

The Null and Alternative Hypotheses

There are two hypotheses that are made: the null hypothesis , denoted H 0 , and the alternative hypothesis , denoted H 1 or H A .

The null hypothesis is the one to be tested and the alternative is everything else. In our example:

The null hypothesis would be: The mean data scientist salary is 113,000 dollars.

While the alternative : The mean data scientist salary is not 113,000 dollars.

Author's note: If you're interested in a data scientist career, check out our articles Data Scientist Career Path , 5 Business Basics for Data Scientists , Data Science Interview Questions , and 15 Data Science Consulting Companies Hiring Now .

An Example of a One-Sided Test

You can also form one-sided or one-tailed tests.

Say your friend, Paul, told you that he thinks data scientists earn more than 125,000 dollars per year. You doubt him, so you design a test to see who’s right.

The null hypothesis of this test would be: The mean data scientist salary is more than 125,000 dollars.

The alternative will cover everything else, thus: The mean data scientist salary is less than or equal to 125,000 dollars.

Important: The outcomes of tests refer to the population parameter rather than the sample statistic! So, the result that we get is for the population.

Important: Another crucial consideration is that, generally, the researcher is trying to reject the null hypothesis . Think about the null hypothesis as the status quo and the alternative as the change or innovation that challenges that status quo. In our example, Paul was representing the status quo, which we were challenging.

Let’s go over it once more. In statistics, the null hypothesis is the statement we are trying to reject. Therefore, the null hypothesis is the present state of affairs, while the alternative is our personal opinion.

Why Hypothesis Testing Works

Right now, you may be feeling a little puzzled. This is normal because this whole concept is counter-intuitive at the beginning. However, there is an extremely easy way to continue your journey of exploring it. By diving into the linked tutorial, you will find out why hypothesis testing actually works.

Interested in learning more? You can take your skills from good to great with our statistics course!

Try statistics course for free

Next Tutorial:  Hypothesis Testing: Significance Level and Rejection Region

Iliya Valchanov

Co-founder of 365 Data Science

Iliya is a finance graduate with a strong quantitative background who chose the exciting path of a startup entrepreneur. He demonstrated a formidable affinity for numbers during his childhood, winning more than 90 national and international awards and competitions through the years. Iliya started teaching at university, helping other students learn statistics and econometrics. Inspired by his first happy students, he co-founded 365 Data Science to continue spreading knowledge. He authored several of the program’s online courses in mathematics, statistics, machine learning, and deep learning.

We Think you'll also like

Statistics Tutorials

False Positive vs. False Negative: Type I and Type II Errors in Statistical Hypothesis Testing

Hypothesis Testing with Z-Test: Significance Level and Rejection Region

Calculating and Using Covariance and Linear Correlation Coefficient

Visualizing Data with Bar, Pie and Pareto Charts