This tutorial is the third in a series of four. This third part shows you how to apply and interpret the tests for ordinal and interval variables. This link will get you back to the first part of the series.
- An ordinal variable contains values that can be ordered like ranks and scores. You can say that one value higher than the other, but you can’t say one value is 2 times more important. An example of this is army ranks: a General is higher in rank than a Major, but you can’t say a General outranks a Major 2 times.
- A interval variable has values that are ordered, and the difference between has meaning, but there is no absolute 0 point, which makes it difficult to interpret differences in terms of absolute magnitude. Money value is an example of an interval level variable, which may sound a bit counterintuitive. Money can take negative values, which makes it impossible to say that someone with 1 million Euros on his bank account has twice as much money as someone that has 1 million Euros in debt. The Big Mac Index is another case in point.

Descriptive
Sometimes you just want to describe one variable. Although these types of descriptions don’t need statistical tests, I’ll describe them here since they should be a part of interpreting the statistical test results. Statistical tests say whether they change, but descriptions on distibutions tell you in what direction they change.
Ordinal median
The median, the value or quantity lying at the midpoint of a frequency distribution, is the appropriate central tendency measure for ordinal variables. Ordinal variables are implemented in R as factor ordered variables. Strangely enough the standard R function median doesn’t support ordered factor variables, so here’s a function that you can use to create this:
Which you can use on the diamond dataset from the ggplot2 library on it’s cut variable, which has the following distribution:
| cut | n() | prop | cum_prop |
|---|---|---|---|
| Fair | 1.610 | 3% | 3% |
| Good | 4.906 | 9% | 12% |
| Very Good | 12.082 | 22% | 34% |
| Premium | 13.791 | 26% | 60% |
| Ideal | 21.551 | 40% | 100% |
With this distribution I’d expect the Premium cut would be the median. Our function call,
shows extactly that:
Ordinal interquartile range
The InterQuartile Range (IQR) is implemented in the IQR function from base R, like it’s median counterpart, does not work with ordered factor variables. So again, we’re out on our own again to create a function for this:
This returns, as expected:
One sample tests are done when you want to find out whether your measurements differ from some kind of theorethical distribution. For example: you might want to find out whether you have a dice that doesn’t get the random result you’d expect from a dice. In this case you’d expect that the dice would throw 1 to 6 about 1/6th of the time.
Wilcoxon one sample test

With the Wilcoxon one sample test, you test whether your ordinal data fits an hypothetical distribution you’d expect. In this example we’ll examine the diamonds data set included in the ggplot2 library. We’ll test a hypothesis that the diamond cut quality is centered around the middle value of “Very Good” (our null hypothesis). First let’s see the total number of factor levels of the cut quality:
The r function for the Wilcoxon one-sample test doesn’t take non-numeric variables. So we have to convert the vector cut to numeric, and ‘translate’ our null hypothesis to numeric as well. As we can derive from the level function’s output the value “Very Good” corresponds to the number 3. We’ll pass this to the wilcox.test function like this:
We can see that our null hypothesis doesn’t hold. The diamond cut quality doesn’t center around “Very Good”. Somewhat non-sensical we also passed TRUE to the argument conf.int , to the function, but this also gave the pseudo median, so we are able to interpret what the cut quality does center around: “Premium” (the level counterpart of the numeric value 4.499967).
Two unrelated samples
Two unrelated sample tests can be used for analysing marketing tests; you apply some kind of marketing voodoo to two different groups of prospects/customers and you want to know which method was best.
Mann-Whitney U test

The Mann–Whitney U test can be used to test whether two sets of unrelated samples are equally distributed. Let’s take our trusted mtcars data set: we can test whether automatic and manual transmission cars differ in gas mileage. For this we use the wilcox.test function:
Since the p-value is well below 0.05, we can assume the cars differ in gas milage between automatic and manual transmission cars. This plot shows us the differences:
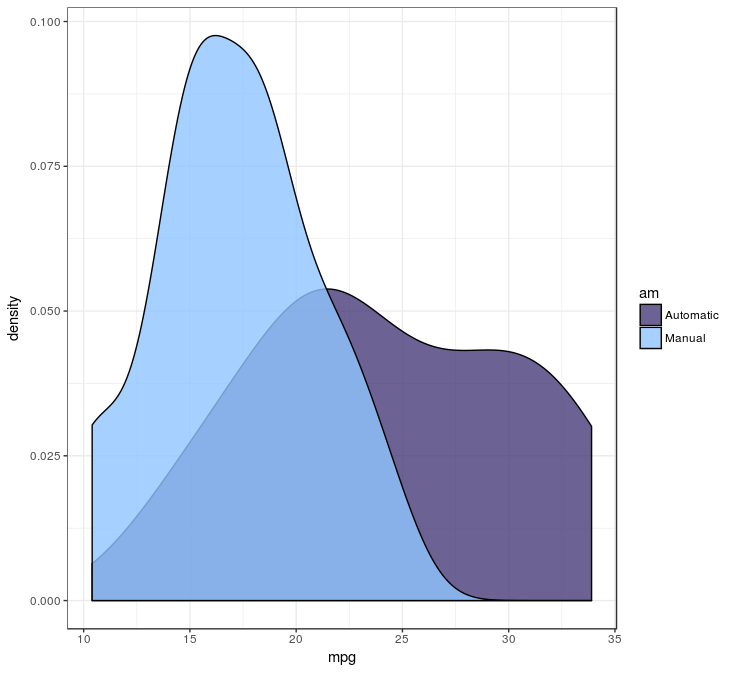
The plot tells us, since the null hypothesis doesn’t hold, it is likely the manual transmission cars have lower gas milage.
Kolmogorov-Smirnov test
The Kolmogorov-Smirnov test tests the same thing as the Mann-Whitney U test, but has a much cooler name; the only reason I included this test here. And I don’t like name dropping, but drop this name in certain circles: it will result in snickers of approval for obvious reasons. The ks.test function call isn’t as elegant as the wilcox.test function call, but still does the job:
Not surprisingly, automatic and manual transmission cars aren’t equal in gas milage, but the p-value is higher than the Mann-Whitney U test told us. This tells us Kolmogorov-Smirnov is a tad more conservative than it’s Mann-Whitney U counterpart.
Two related samples
Related samples tests are used to determine whether there are differences before and after some kind of treatment. It is also useful when seeing when verifying the predictions of machine learning algorithms.
Wilcoxon Signed-Rank Test
The Wilcoxon Signed-Rank Test is used to see whether observations changed direction on two sets of ordinal variables. It’s usefull, for example, when comparing results of questionaires with ordered scales for the same person across a period of time.
Association between 2 variables
Tests of association determine what the strength of the movement between variables is. It can be used if you want to know if there is any relation between the customer’s amount spent, and the number of orders the customer already placed.
Spearman Rank Correlation

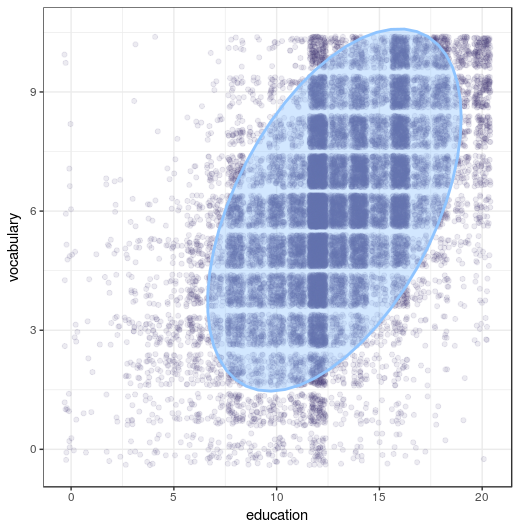
The Spearman Rank Correlation is a test of association for ordinal or interval variables. In this example we’ll see if vocabulary is related to education. The function cor.test can be used to see if they are related:
It looks like there is a relation between education and vocubulary. By looking at the plot, you can see the relation between education and vocabulary is a quite positive one.
Association measures can be useful more than one variable at a time. For example you might want to consider a range of variables from your data set for inclusion in your predictive model. Luckily the corrplot library contains the corrplot_function to quickly visualise the relations between all in a dataset. Let’s take the mtcars variables as an example:
The matrix mat_corr contains all Spearman rank correlation values, which are calculated with the cor function, passing the whole data frame of mtcars , using the method spearman and only include the pairwise observations. Then the p-values of each of the correlations are calculated using *corrplot**’s cor.mtest function, with the same function arguments. Both are used in the corrplot function, where the order , type and cl.post arguments specify some layout, which I won’t go in further. The argument p.mat is the p-value matrix, which are used by the sig.level and insig arguments to leave out those correlations which are considered insigificant below the 0.05 threshold.
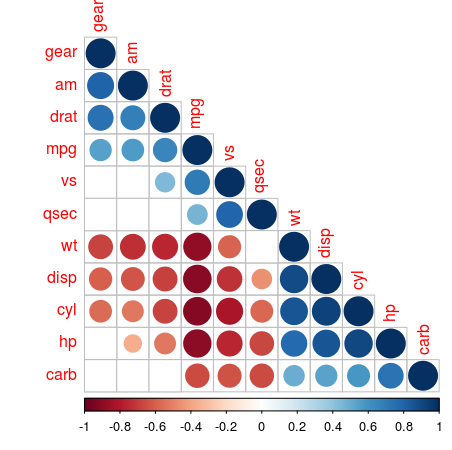
This plot shows which values are positively correlated by the blue dots, while the negative associations are indicated by red dots. The size of the dots and the intensity of the colour show how strong that association is. The cells without dot, don’t have significant correlations. For the number of cylinders ( cyl ) are strongly negatively correlated with the milage per gallon, while the horsepower ( hp ) is positively associated with the number of carburetors ( carb ) albeit not as strong.
When you make a correlation martrix like this, be on the lookout for spurious correlations . Putting in variables into your model indiscriminately, without reasoning, may lead to some unintended results…
4: Tests for Ordinal Data and Small Samples
So far, we've dealt with the concepts of independence and association in two-way tables assuming nominal classification. The Pearson and likelihood test statistics introduced do not assume any particular ordering of the rows or columns, and their numeric values do not change if the ordering is altered in any way. If a natural ordering exists (i.e., for ordinal data), we can utilize it to potentially increase the power of our tests. In the last section, we will consider a test proposed by R. A. Fisher for two-way tables that is applicable when the sample size is small and/or cell counts are small, and the large-sample methodology does not hold. But before getting into testing and inference, we revisit some measures of association and see how they can accommodate ordinal data.
Lesson 4 Code Files
- MantelHaenszel.R
- TeaLady.sas
- ordinal.sas
Useful Links
- SAS documentation for PROC FREQ
4.1 - Cumulative Odds and Odds Ratios
Recall that a discrete ordinal variable, say \(Y\), takes on values that can be sorted either least to greatest or greatest to least. Examples introduced earlier might be the face of a die (\(1,2,\ldots,6\)) or a person's attitude towards war ("strongly disagree", "disagree", "agree", "strongly agree"). For convenience, we may label such categories as 1 through \(J\), which allows us to express cumulative probabilities as
\(F(j) = P(Y\le j)=\pi_1+\cdots+\pi_j\),
where the parameter \(\pi_j\) represents the probability of category \(j\). So, we can write \(F(2)=\pi_1+\pi_2\) to represent the probability that the die is either 1 or 2, or, in the second example, the probability that an individual responds either "strongly disagree" or "disagree". Note that we need only the ordinal property for this to make sense; the values \(1,2,\ldots,J\) themselves do not represent any numerically meaningful quantities in these cases.
Cumulative Odds
In addition to probabilities (or risks), ordinal categories also allow an odds to be defined for cumulative events. Recall the observed data for the war attitude example:
| Attitude | Count |
|---|---|
| Strongly disagree | 35 |
| Disagree | 27 |
| Agree | 23 |
| Strongly agree | 31 |
| Total | 116 |
If we focus on the "disagree" outcome in particular, the estimated probability would be \(\hat{\pi}_2=27/116=0.2328\) with corresponding estimated odds \(\hat{\pi}_2/(1-\hat{\pi}_2)=27/(35+23+31)=0.3034\). However, using the estimated cumulative probability \(\hat{F}(2)=\hat{\pi}_1+\hat{\pi}_2=(35+27)/116=0.5345\), we may also consider the estimated cumulative odds:
\( \dfrac{\hat{F}(2)}{1-\hat{F}(2)}=\dfrac{35+27}{23+31}=1.1481 \)
We interpret this value as the (estimated) cumulative odds that an individual will "disagree", where the category of "strongly disagree" is implicitly included. Equivalently, we may also refer to this as the (estimated) odds of "strongly disagree" or "disagree". In general, we define the cumulative odds for \(Y\le j\) as
\(\dfrac{F(j)}{(1-F(j))}=\dfrac{\pi_1+\cdots+\pi_j}{\pi_{j+1}+\cdots+\pi_J},\quad\mbox{for }j=1,\ldots,J-1\)
with sample estimate \(\hat{F}(j)/(1-\hat{F}(j))\). The case \(j=J\) is not defined because \(1-F(J)=0\). Like cumulative probabilities, cumulative odds are necessarily non-decreasing and will be strictly increasing if the observed counts are all positive.
Cumulative Odds Ratios
If an additional variable is involved, this idea extends to cumulative odds ratios. Consider the table below summarizing the responses for extent of agreement to the statement "job security is good" ( jobsecok ) and general happiness ( happy) from the 2018 General Social Surveys. Additional possible responses of "don't know" and "no answer" are omitted here.
| Not too happy | Pretty happy | Very happy | |
|---|---|---|---|
| Not at all true | 15 | 25 | 5 |
| Not too true | 21 | 47 | 21 |
| Somewhat true | 64 | 248 | 100 |
| Very true | 73 | 474 | 311 |
If we condition on jobsecok and view happy as the response variable, the cumulative odds ratio for "not too happy" or "pretty happy" for those who say "not at all true", relative to those who say "very true", would be estimated with
\(\dfrac{(15+25)/5}{(73+474)/311}=4.55 \)
If perhaps "pretty happy" and "very happy" seem like a more intuitive combination to consider, keep in mind that we're free to reverse the order to start with "very happy" and end with "not too happy" without violating the ordinal nature of this variable. By indexing "very happy" with \(j=1\), \(F(2)\) becomes the cumulative probability of "very happy" or "pretty happy", and the cumulative odds would likewise be \(F(2)/(1-F(2))\). Likewise, we could choose any two rows to serve as the groups for comparison. The row variable doesn't even have to be ordinal itself to define such a cumulative odds ratio.
However, if we happen to have two ordinal variables, as we do in this example, we can work with a cumulative version in both dimensions. We may, for example, consider the cumulative odds of "not too happy" or "pretty happy", for those who say "not at all" or "not too" true, relative to those who say "somewhat" or "very" true. The estimate of this would be
\(\dfrac{(15+25+21+47)/(5+21)}{(64+248+73+474)/(100+311)}=1.99 \)
The common theme in all these odds ratios is that they essentially convert an \(I\times J\) table into a \(2\times2\) table by combining or "accumulating" counts in adjacent categories, depending on our focus of interest. This is illustrated by the shading in the tables below.
| Not too happy | Pretty happy | Very happy | |
|---|---|---|---|
| Not at all true | 15 | 25 | 5 |
| Not too true | 21 | 47 | 21 |
| Somewhat true | 64 | 248 | 100 |
| Very true | 73 | 474 | 311 |
| Not too or pretty happy | Very happy | |
|---|---|---|
| Not at all true | 40 | 5 |
| Very true | 547 | 311 |
| Not too or pretty happy | Very happy | |
|---|---|---|
| Not at all or not too true | 108 | 26 |
| Somewhat or very true | 859 | 411 |
CIs for Cumulative Odds Ratios
Recall for a \(2\times 2\) table with counts \((n_{11},n_{12},n_{21},n_{22})\), we have the sample odds ratio \(\dfrac{n_{11}n_{22}}{n_{12}n_{21}}\) and corresponding 95% confidence interval for the (population) log odds ratio:
\(\log\dfrac{n_{11}n_{22}}{n_{12}n_{21}} \pm 1.96\sqrt{\dfrac{1}{n_{11}}+\dfrac{1}{n_{12}}+\dfrac{1}{n_{21}}+\dfrac{1}{n_{22}}}\)
We can readily adopt this formula for a cumulative odds ratio \(\theta\) as well. We just need to work with the \(2\times2\) table of counts induced by any accumulation. For example, the \(2\times2\) table induced by the cumulative odds ratio for "not too" or "pretty" happy for those saying "not at all" compared with "very" true is
| Not too or Pretty happy | Very happy | |
|---|---|---|
| Not at all true | 40 | 5 |
| Very true | 547 | 311 |
With estimate \(\hat{\theta}=4.55\), the 95% confidence interval for \(\log\theta\) is
\(\log 4.55 \pm 1.96\sqrt{\dfrac{1}{40}+\dfrac{1}{5}+\dfrac{1}{547}+\dfrac{1}{311}} = (0.5747, 2.4549)\)
And by exponentiating the endpoints, we have the 95% CI for \(\theta\):
\(e^{(0.5747, 2.4549)}=(1.7766, 11.6448)\)
Likewise, for the cumulative odds of "not too" or "pretty" happy, for those saying "not at all" or "not too" true compared with those saying "somewhat" or "very" true, we have on the log scale
\(\log 1.99 \pm 1.96\sqrt{\dfrac{1}{108}+\dfrac{1}{26}+\dfrac{1}{859}+\dfrac{1}{411}} = (0.2429, 1.1308)\)
And, by exponentiating limits, we have the final CI for the odds ratio:
\(e^{(0.2429, 1.1308)}=(1.275, 3.098)\)
To put it a bit more loosely, we can say that individuals who generally don't agree as much with the statement "job security is good" have a greater odds of being less happy. Or, equivalently, those who generally agree more with the statement "job security is good" have a greater odds of being happier.
4.2 - Measures of Positive and Negative Association
While two nominal variables can be associated (knowing something about one can tell us something about the other), without a natural ordering, we can't specify that association with a particular direction, such as positive or negative. With an ordinal variable, however, it makes sense to think of one of its outcomes as being "higher" or "greater" than another, even if they aren't necessarily numerically meaningful. And with two such ordinal variables, we can define a positive association to mean that both variables tend to be either "high" or "low" together; a negative association would exist if one tends to be "high" when the other is "low". We solidify these ideas in this lesson.
Concordance and Gamma
With this notion of "high" and "low" available for two (ordinal) variables \(X\) and \(Y\), we can define a quantity that measures both strength and direction of association. Suppose that \(X\) takes on the values \(1,2,\ldots,I\) and that \(Y\) takes on the values \(1,2,\ldots,J\). We can think of these as ranks of the categories in each variable once we have decided which direction "high" corresponds to. As we've seen already, the direction of the ordering is somewhat arbitrary. The "highest" category for happy could just as easily be "very happy" as "not too happy", as long as adjacent categories are kept together. One direction is often more intuitive than the other, however.
If \((i,j)\) represents an observation in the \(i\)th row and \(j\)th column (i.e., \(X=i\) and \(Y=j\) for that observation), then the pair of observations \((i,j)\) and \((i',j')\) are concordant if
\((i-i')(j-j')>0\)
If \((i-i')(j-j')<0\), then the pair is discordant . If either \(i=i'\) or \(j=j'\), then neither term will be used---effectively, ties in either \(X\) or \(Y\) are ignored. If \(C\) and \(D\) denote the number of concordant and discordant pairs, respectively, then a correlation-like measure of association between \(X\) and \(Y\) due to Goodman and Kruskal (1954) is
\(\hat{\gamma}=\dfrac{C-D}{C+D}\)
Like the usual sample correlation between quantitative variables, \(\hat{\gamma}\) always falls within \([-1,1]\) and indicates stronger positive (or negative) association the closer it is to \(+1\) (or \(-1)\).
In our example from the 2018 GSS, respondents were asked to rate their agreement to the statement "Job security is good" with respect to the work they were doing ( jobsecok ). For the concordance calculations, the responses "not at all true", "not too true", "somewhat true", and "very true" are interpreted as increasing in job security. Similarly, the responses for general happiness ( happy ) "not too happy", "pretty happy", and "very happy" are interpreted as increasing in happiness. Recall the observed counts for these variables below.
| Not too happy | Pretty happy | Very happy | |
|---|---|---|---|
| Not at all true | 15 | 25 | 5 |
| Not too true | 21 | 47 | 21 |
| Somewhat true | 64 | 248 | 100 |
| Very true | 73 | 474 | 311 |
First, we'll count the number of concordant pairs of individuals (observations). Consider first an individual from cell \((1,1)\) paired with an individual from cell \((2,2)\). This pair is concordant because
\((2-1)(2-1)>0\)
That is, the first individual has lower values for both happy ("not too happy") and jobsecok ("not at all true"). Moreover, this result holds for all pairs consisting of one individual chosen from the 15 in cell \((1,1)\) and one individual chosen from the 47 in cell \((2,2)\). Since there are \(15(47)=705\) such pairings, we've just counted 705 concordant pairs!
By the same argument, pairs chosen from cells \((1,1)\) and \((2,3)\) contribute \(15(21)=315\), pairs chosen from cells \((1,1)\) and \((3,2)\) contribute \(15(248)=3720\), and so. If we're careful to skip over pairs for which any ties occur, our final count should be \(C=199,293\).
Counting discordant pairs works in a similar way. For example, a pair from cells \((1,2)\) and \((2,1)\) are discordant because
\((2-1)(1-2)<0\)
This pair contributes to a negative relationship because the first individual provided a lower value for jobsecok ("not at all true") but a higher value for happy ("pretty happy"), relative to the second individual. And all \(25(21)=525\) such pairs of individuals are counted likewise. Again, without consideration of tied values, we can count a total of \(D=105,867\) discordant pairs in this table. And as a final summary, the gamma correlation value is
\(\hat{\gamma}=\dfrac{199293-105867}{199293+105867}=0.30615\)
This represents a relatively weak positive association between perceived job security and happiness.
Kendall's Tau and Tau-b
Another way to measure association for two ordinal variables is due to Kendall (1945) and incorporates the number of tied observations. With categorical variables, such as happiness or opinion on job security, many individuals will agree or "tie" in either the row variable, the column variable, or both. If we let \(T_r\) and \(T_c\) represent the number of pairs that are tied in the row variable and column variable, respectively, then we can count from the row and column totals
\(T_r=\sum_{i=1}^I\dfrac{n_{i+}(n_{i+}-1)}{2}, \) and \(T_c=\sum_{j=1}^J\dfrac{n_{+j}(n_{+j}-1)}{2} \)
Moreover, if \(n\) denotes the total number of observations in the sample, then Kendall's tau-b is calculated as
\( \hat{\tau}_b=\dfrac{C-D}{\sqrt{[n(n-1)/2-T_r][n(n-1)/2-T_c]}} \)
Like gamma, tau-b is a correlation-like quantitative that measures both strength and association of two ordinal variables. It always falls within \([-1,1]\) with stronger positive (or negative) association corresponding to \(+1\) (or \(-1\)). However, the denominator for tau-b is generally larger than that for gamma so that tau-b is generally weaker (closer to 0 in absolute value). To see why this is, note that \({n\choose2}=n(n-1)/2\) represents the total number of ways to choose two observations from the grand total and can be expanded as
\(\dfrac{n(n-1)}{2}=C+D+T_r+T_c-T_{rc} \)
where \(T_{rc}\) is the number of pairs of observations (from the diagonal counts) that tie on both the row and column variable. In other words, tau-b includes some ties in its denominator, while gamma does not, and ties do not contribute to either a positive or negative association.
It should also be noted that if there are no ties (i.e., every individual provides a unique response), both gamma and tau-b reduce to
\( \hat{\tau}=\dfrac{C-D}{n(n-1)/2} \)
which is known simply as Kendall's tau and is usually reserved for continuous data that has been converted to ranks. In the case of categorical variables, ties are unavoidable.
For the data above regarding jobsecok and happy , we find
\(T_r=\dfrac{45(44)+89(88)+412(411)+858(857)}{2} =457225,\) and \(T_c=\dfrac{173(172)+794(793)+437(436)}{2} =424965\)
and then, with \(n=1404\), calculate Kendall's tau-b to be
\( \hat{\tau}_b=\dfrac{199293-105867}{\sqrt{[1404(1403)/2-457225][1404(1403)/2-424965]}}=0.1719 \)
Thus, both gamma and tau-b estimate the relationship between jobsecok and happy to be moderately positive.
Code
The R code to carry out the calculations above:
4.3 - Measures of Linear Trend
So far, we've referred to both gamma and tau-b as "correlation-like" in that they measure both the strength and the direction of an association. The correlation in reference is Pearson's Correlation , or Pearson's correlation coefficient . As a parameter, Pearson's correlation is defined for two (quantitative) random variables Y and Z as
\( \rho=\dfrac{Cov(Y,Z)}{\sigma_Y\sigma_Z} \)
where \(Cov(Y,Z)=E[(Y-\mu_Y)(Z-\mu_Z)]\) is the covariance of \(Y\) and \(Z\). To see intuitively how this measures linear association, notice that \((Y-\mu_Y)(Z-\mu_Z)\) will be positive if \(Y\) and \(Z\) tend to be large (greater than their means) or tend to be small (less than their means) together. Dividing by their standard deviations removes the units involved with the variables results in a quantity that always falls within \([-1,1]\). The sample estimate of \(\rho\) is
\(r = \dfrac{(n-1)^{-1}\sum_{i=1}^n(Y_i-\overline{Y})(Z_i-\overline{Z})}{s_Ys_Z} \)
where \(s_Y\) and \(s_Z\) are the sample standard deviations of \(Y\) and \(Z\), respectively. Both the population \(\rho\) and the sample estimate \(r\) satisfy the following properties:
- \(−1 \le r \le 1\)
- \(r = 0\) corresponds to no (linear) relationship
- \(r = \pm1\) corresponds to perfect association, which for a two-way (square) table means that all observations fall into the diagonal cells.
When classification is ordinal, we can sometimes assign quantitative or numerically meaningful scores to the categories, which allows Pearson's correlation to be defined and estimated. The null hypothesis of interest in such a situation is whether the correlation is 0, meaning specifically that there is no linear trend among the ordinal levels. If the null hypothesis of (linear) independence is rejected, it is natural and meaningful to then measure the linear trend. It should be noted that the correlation considered is defined from the scores of the categories. Different choices of scores will generally result in different correlation measures.
A common approach to assigning scores to \(J\) ordered categories is to use their ranks: \(1,2,\ldots,J\) from least to greatest. Pearson's correlation formula applied to this choice of scores is known as Spearman's correlation (Spearman's rho) . Even when the variables are originally quantitative, Spearman's rho is a popular non-parametric choice because it's not influenced by outliers. For example, the values 3.2, 1.8, and 4.9 have the same ranks (2, 1, 3) as the values 3.2, 1.8 and 49.0. We've encountered this idea of ranks already in our discussion of cumulative odds, but the difference here is that scores are treated as numerically meaningful and, if two variables are scored as such, will define a correlation that measures linear association.
For the 2018 GSS survey data relating jobsecok to happy , we can assign the scores (1,2,3,4) going down the rows to indicate increasing agreement (to the statement on job security) and scores (1,2,3) going across the columns from left to right to indicate increasing happiness.
| 1 | 2 | 3 | |
|---|---|---|---|
| 1 | 15 | 25 | 5 |
| 2 | 21 | 47 | 21 |
| 3 | 64 | 248 | 100 |
| 4 | 73 | 474 | 311 |
The correlation calculated from these scores is then 0.1948, which represents a relatively weak positive, linear association.
Assigning Scores
As an alternative to scores based on ranks, we may have another choice that appropriately reflects the nature of the ordered categories. In general, we denote scores for the categories of the row variable by \(u_1 \le u_2 \le\cdots\le u_I\) and of the column variable by \(v_1\le v_2 \cdots\le v_J\). This defines a correlation as a measure of linear association between these two scored variables and can be estimated with the same formula used for Pearson's correlation. For an \(I\times J\) table with cell counts \(n_{ij}\), this estimate is
\(r=\dfrac{\sum_i\sum_j(u_i-\bar{u})(v_j-\bar{v})n_{ij}}{\sqrt{[\sum_i\sum_j(u_i-\bar{u})^2 n_{ij}][\sum_i\sum_j(v_j-\bar{v})^2n_{ij}]}}\)
where \(\bar{u}=\sum_i\sum_j u_i n_{ij}/n\) is the row mean, and \(\bar{v}=\sum_i\sum_j v_j n_{ij}/n\) is the column mean.
Note that the assignment of scores is arbitrary and will in general influence the resulting correlation. As a demonstration of this in our current example, suppose we assign the scores (1,2,9,10) to jobsecok and the scores (1,9,10) to happy . Such a choice would make sense if the response categories were spaced more erratically. The resulting correlation would be \(r=0.1698\).
Thus, to avoid "data-snooping" or artificially significant results, scores should be assigned first, chosen thoughtfully to reflect the nature of the data, and results should be interpreted precisely in terms of the scores that were chosen.
Midrank Scores
If the row and column totals of the table are highly unbalanced, different scores can produce large differences in the estimated correlation \(r\). One option for assigning scores that accounts for this is to use midranks . The idea is based on ranks, but instead of assigning 1, 2, etc. to the categories directly, the ranks are first assigned to the individuals \(1,2,\ldots,n\) for each variable, and then category scores are calculated based on the average rank for the individuals in that category.
For an \(I\times J\) table with \(n_{i+}\) and \(n_{+j}\) representing the row and column totals, respectively, the midrank score for the 1st category of the row variable is
\(u_1=\dfrac{1+2+\cdots+n_{1+}}{n_{1+}} \)
For the second category, we also assign the average rank of the individuals, but note that the ranks begin where they ended in the first category:
\(u_2=\dfrac{(n_{1+}+1)+\cdots+(n_{1+}+n_{2+})}{n_{2+}} \)
And in general, this formula is expressed as
\(u_i=\dfrac{(\sum_{k=1}^{i-1}n_{k+}+1)+\cdots+(\sum_{k=1}^{i}n_{k+})}{n_{i+}} \)
Similarly, midrank scores for the column variable are based on column totals. Ultimately, we end up with \((u_1,\ldots,u_I)\) for the row variable and \((v_1,\ldots,v_J)\) for the column variable, but the values and the spacing of these scores depends on the number of individuals in each category. Let's see how this works for the 2018 GSS example.
The first row corresponds to the \(n_{1+}=45\) individuals replying "Not at all true". If they were individually ranked from 1 to 45, the average of these ranks would be \(u_1=(1+\cdots+45)/45=23\). Likewise, the \(n_{2+}=89\) individuals in the second row would be ranked from 46 to 134 with average rank \(u_2=(46+\cdots+134)/89=90\). Continuing in this way, we find the midrank scores for jobsecok to be \((23,90,340.5,975.5)\) and those for happy to be \((87,570.5,1186)\), from which we can calculate the correlation \(0.1849\).
4.4 - Mantel-Haenszel Test for Linear Trend
For a given set of scores and corresponding correlation \(\rho\), we can carry out the test of \(H_0\colon\rho=0\) versus \(H_A\colon\rho\ne0\) using the Mantel-Haenszel (MH) statistic :
\(M^2=(n-1)r^2\)
where \(n\) is the sample size (total number of individuals providing both row and column variable responses), and \(r\) is the sample estimate of the correlation from the given scores. Additional properties are as follows:
- When \(H_0\) is true, \(M^2\) has an approximate chi-square distribution with 1 degree of freedom, regardless of the size of the two-way table.
- \(\mbox{sign}\cdot(r)|M|\) has an approximate standard normal distribution, which can be used for testing one-sided alternatives too. Note that we use the sign of the sample correlation, so this test statistic may be either positive or negative.
- Larger values of \(M^2\) provide more evidence against the linear independence model.
- The value of \(M^2\) (and hence the evidence to reject \(H_0\)) increases with both sample size \(n\) and the absolute value of the estimated correlation \(|r|\).
Now, we apply the Mantel-Haenszel test of linear relationship to the 2018 GSS variables jobsecok and happy . There are two separate R functions we can run, depending on whether we want to input scores directly ( MH.test ) or whether we want R to use the midranks ( MH.test.mid ). Both functions are defined in the file MantelHaenszel.R , so we need to run that code first.
For the scores \((1,2,3,4)\) assigned to jobsecok and \((1,2,3)\) assigned to happy , the correlation estimate is \(r=0.1948\) (slightly rounded), and with \(n=1404\) total observations, we calculate \(M^2=(1404-1)0.1948^2=53.248\), which R outputs, along with the \(p\)-value indicating extremely significant evidence that the correlation between job security and happiness is greater than 0, given these particular scores. Similarly, if the midranks are used, the correlation estimate becomes \(r=0.1849\) with MH test statistic \(M^2=47.97\). The conclusion is unchanged.
The R code to carry out the calculations above:
If we search for a built-in function in R to compute the MH test statistic, we will find a few additional functions, such as the mantelhaen.test. However, this is a different test and is designed to work with \(2\times2\times K\) tables to measure conditional association, which we'll see later.
Power vs Pearson Test of Association
When dealing with ordinal data, when there is a positive or negative linear association between variables, the MH test has a power advantage over the Pearson or LRT test that treats the categories as nominal, meaning the MH test is more likely to detect such an association when it exists. Here are some other comparisons between them.
- The Pearson and LRT tests consider the most general alternative hypothesis for any type of association. The degrees of freedom, which is the number of parameters separating the null and alternative models, is relatively large at \((I − 1)(J − 1)\).
- The MH test has only a single degree of freedom, reflecting the fact that the correlation is the only parameter separating the null model of independence from the alternative of linear association. The critical values (thresholds for establishing significance) will generally be smaller, compared with critical values from a chi-squared distribution with \((I-1)(J-1)\) degrees of freedom.
- For small to moderate sample size, the sampling distribution of \(M^2\) is better approximated by a chi-squared distribution than are the sampling distributions for \(X^2\) and \(G^2\), the Pearson and LRT statistics, respectively; this tends to hold in general for distributions with smaller degrees of freedom.
Since the MH test assumes from the beginning that the association is linear, it may not be as effective in detecting associations that are not linear. Consider the hypothetical table below relating the binary response (success, failure) to the level of drug applied (low, medium, high).
| Success | Failure | |
|---|---|---|
| 5 | 15 | |
| 10 | 10 | |
| 5 | 15 |
Treating these categories as nominal, the Pearson test statistic would be \(X^2=3.75\) with \(p\)-value 0.1534 relative to chi-square distribution with two degrees of freedom. By contrast, with scores of \((1,2,3)\) assigned to the drug levels and \((1,2)\) assigned to the binary outcomes, the MH test statistic for linear association would be \(M^2=0\) with \(p\)-value 1, indicating no evidence for linear association. The reason the MH test fails to find any evidence is that it's looking specifically for increasing or decreasing trends consistent with stronger correlation values, which is not present in this data. The success rate increases from low to medium drug level but then decreases from medium to high. The Pearson test is more powerful in this situation because it is essentially measuring whether there is any change in success rates.
Not surprisingly, if the table values were observed to be those below, where the success rates are increasing from drug levels low to high, the MH test would be more powerful (\(X^2=10.0\) with \(p\)-value 0.0067 versus \(M^2=9.83\) with \(p\)-value 0.0017).
| Success | Failure | |
|---|---|---|
| 5 | 15 | |
| 10 | 10 | |
| 15 | 5 |
The takeaway point from this is that the MH test is potentially more powerful than the Pearson (or LRT) if the association between the variables is linear. Even if the ordered categories can be assigned meaningful scores, it doesn't guarantee that the variables' association is linear.
Finally, although we did use the scores \((1,2)\) for the binary outcome, this choice is inconsequential for calculating a correlation involving a variable with only two categories, meaning that we would get the same value for the MH test statistic with any choice of scores. If the outcome variable had three or more categories, however, they would need to be ordinal with appropriately assigned scores for the MH test to be meaningful.
4.5 - Fisher's Exact Test
The tests discussed so far that use the chi-square approximation, including the Pearson and LRT for nominal data as well as the Mantel-Haenszel test for ordinal data, perform well when the contingency tables have a reasonable number of observations in each cell, as already discussed in Lesson 1. When samples are small, the distributions of \(X^2\), \(G^2\), and \(M^2\) (and other large-sample based statistics) are not well approximated by the chi-squared distribution; thus their \(p\) - values are not to be trusted. In such situations, we can perform inference using an exact distribution (or estimates of exact distributions), but we should keep in mind that \(p\) - values based on exact tests can be conservative (i.e, measured to be larger than they really are).
We may use an exact test if:
- the row totals \(n_{i+}\) and the column totals \(n_{+j}\) are both fixed by design of the study.
- we have a small sample size \(n\),
- more than 20% of cells have expected cell counts less than 5, and no expected cell count is less than 1.
Example: Lady tea tasting

Here we consider the famous tea tasting example! In a summer tea-part in Cambridge, England, a lady claimed to be able to discern, by taste alone, whether a cup of tea with milk had the tea poured first or the milk poured first. An experiment was performed by Sir R.A. Fisher himself, then and there, to see if her claim was valid. Eight cups of tea were prepared and presented to her in random order. Four had the milk poured first, and other four had the tea poured first. The lady tasted each one and rendered her opinion. The results are summarized in the following \(2 \times 2\) table:
| Actually poured first | Lady says poured first | |
|---|---|---|
| tea | milk | |
| tea | 3 | 1 |
| milk | 1 | 3 |
The row totals are fixed by the experimenter. The column totals are fixed by the lady, who knows that four of the cups are "tea first" and four are "milk first." Under \(H_0\), the lady has no discerning ability, which is to say the four cups she calls "tea first" are a random sample from the eight. If she selects four at random, the probability that three of these four are actually "tea first" comes from the hypergeometric distribution, \(P(n_{11}=3)\):
\(\dfrac{\dbinom{4}{3}\dbinom{4}{1}}{\dbinom{8}{4}}=\dfrac{\dfrac{4!}{3!1!}\dfrac{4!}{1!3!}}{\dfrac{8!}{4!4!}}=\dfrac{16}{70}=0.229\)
A \(p\)-value is the probability of getting a result as extreme or more extreme than the event actually observed, assuming \(H_0\) is true. In this example, the \(p\)-value would be \(P(n_{11}\ge t_0)\), where \(t_0\) is the observed value of \(n_{11}\), which in this case is 3. The only result more extreme would be the lady's (correct) selection of all four the cups that are truly "tea first," which has probability
\(\dfrac{\dbinom{4}{4}\dbinom{4}{0}}{\dbinom{8}{4}}=\dfrac{1}{70}=0.014\)
As it turns out, the \(p\)-value is \(.229 + .014 = .243\), which is only weak evidence against the null. In other words, there is not enough evidence to reject the null hypothesis that the lady is just purely guessing. To be fair, experiments with small amounts of data are generally not very powerful, to begin with, given the limited information.
Here is how we can do this computation in SAS and R. Further below we describe in a bit more detail the underlying idea behind these calculations.
The SAS System
The FREQ Procedure
Statistics for Table of poured by lady
Sample Size = 8 OPTION EXACT in SAS indicates that we are doing exact tests which consider ALL tables with the exact same margins as the observed table. This option will work for any \(I \times J\) table. OPTION FISHER, more specifically performs Fisher's exact test which is an exact test only for a \(2 \times 2\) table in SAS. For R, see TeaLady.R where you can see we used the fisher.test() function to perform Fisher's exact test for the \(2 \times 2\) table in question. The same could be done using chisq.test() with option, simulate.p.value=TRUE . By reading the help file on fisher. test() function, you will see that certain options in this function only work for \(2 \times 2\) tables. For the output, see TeaLady.out The basic idea behind exact tests is that they enumerate all possible tables that have the same margins, e.g., row sums and column sums. Then to compute the relevant statistics, e.g., \(X^2\), \(G^2\), odds-ratios, we look for all tables where the values are more extreme than the one we have observed. The key here is that in the set of tables with the same margins, once we know the value in one cell, we know the rest of the cells. Therefore, to find a probability of observing a table, we need to find the probability of only one cell in the table (rather than the probabilities of four cells). Typically we use the value of cell (1,1). Under the null hypothesis of independence, more specifically when odds-ratio \(\theta = 1\), the probability distribution of that one cell \(n_{11}\) is hypergeometric, as discussed in the Tea lady example. Stop and Think!Extension of fisher's test. For problems where the number of possible tables is too large, Monte Carlo methods are used to approximate "exact" statistics (e.g., option MC in SAS FREQ EXACT and in R under chisq.test() you need to specify simulate.p.value = TRUE and indicate how many runs you want MC simulation to do; for more see the help files). This extension, and thus these options in SAS and R, of the Fisher's exact test for a \(2 \times 2\) table, in effect, takes samples from a large number of possibilities in order to simulate the exact test. This test is "exact" because no large-sample approximations are used. The \(p\)-value is valid regardless of the sample size. Asymptotic results may be unreliable when the distribution of the data is sparse, or skewed. Exact computations are based on the statistical theory of exact conditional inference for contingency tables. Fisher's exact test is definitely appropriate when the row totals and column totals are both fixed by design. Some have argued that it may also be used when only one set of margins is truly fixed. This idea arises because the marginal totals \(n_{1+}, n_{+1}\) provide little information about the odds ratio \(\theta\). Exact non-null inference for \(\theta\)When \(\theta = 1\), this distribution is hypergeometric, which we used in Fisher's exact test. More generally, Fisher (1935) gave this distribution for any value of \(\theta\). Using this distribution, it is easy to compute Fisher's exact \(p\)-value for testing the null hypothesis \(H_0:\theta=\theta^*\) for any \(\theta^*\). The set of all values \(\theta^*\) that cannot be rejected at the \(\alpha=.05\) level test forms an exact 95% confidence region for \(\theta\). Let's look at a part of the SAS output a bit closer, we get the same CIs in the R ouput. First, notice the sample estimate of the odds ratio equal to 9, which we can compute from the cross-product ratio as we have discussed earlier. Note also that fisher.test() in R for \(2 \times 2\) tables will give so-called "conditional estimate" of the odds-ratio so the value will be different (in this case, approximately 6.408). Notice the difference between the exact and asymptotic CIs for the odds ratio for the two-sided alternative (e.g., \(\theta\ne1\)). The exact version is larger. Recalling the interpretation of the odds ratio, what do these CIs tell us about true unknown odds-ratio? This is a simple example of how inference may vary if you have small samples or sparseness. Bias correction for estimating \(\theta\)Earlier, we learned that the natural estimate of \(\theta\) is \(\hat{\theta}=\dfrac{n_{11}n_{22}}{n_{12}n_{21}}\) and that \(\log\hat{\theta}\) is approximately normally distributed about \(\log \theta\) with estimated variance \(\hat{V}(\log\hat{\theta})=\dfrac{1}{n_{11}}+\dfrac{1}{n_{12}}+\dfrac{1}{n_{21}}+\dfrac{1}{n_{22}}\) Advanced note: this is the estimated variance of the limiting distribution, not an estimate of the variance of \(\log\hat{\theta}\) itself. Because there is a nonzero probability that the numerator or the denominator of \(\hat{\theta}\) may be zero, the moments of \(\hat{\theta}\) and \(\log\hat{\theta}\) do not actually exist. If the estimate is modified by adding \(1/2\) to each \(n_{ij}\), we have \(\tilde{\theta}=\dfrac{(n_{11}+0.5)(n_{22}+0.5)}{(n_{12}+0.5)(n_{21}+0.5)}\) with estimated variance \(\hat{V}(\log\tilde{\theta})=\sum\limits_{i,j} \dfrac{1}{(n_{ij}+0.5)}\) In smaller samples, \(\log\tilde{\theta}\) may be slightly less biased than \(\log\hat{\theta}\). 4.6 - Lesson 4 SummaryIn this lesson, we extended the idea of association in two-way contingency tables to accommodate ordinal data and linear trends. The key concepts are that ordinal data has a particular nature that we can summarize and potentially take advantage of when carrying out a significance test. We also introduced an alternative "exact" test for \(2\times2\) tables that can be used when the observed counts are too small for the usual chi-square approximation to apply. Coming up next, we consider new ways to measure associations if more than two variables are in the picture. Specifically, we'll see how one relationship can be confounded with another so that interpretations will change, depending on whether we condition on certain variables in advance. Have a language expert improve your writingRun a free plagiarism check in 10 minutes, generate accurate citations for free.
Hypothesis Testing | A Step-by-Step Guide with Easy ExamplesPublished on November 8, 2019 by Rebecca Bevans . Revised on June 22, 2023. Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics . It is most often used by scientists to test specific predictions, called hypotheses, that arise from theories. There are 5 main steps in hypothesis testing:
Though the specific details might vary, the procedure you will use when testing a hypothesis will always follow some version of these steps. Table of contentsStep 1: state your null and alternate hypothesis, step 2: collect data, step 3: perform a statistical test, step 4: decide whether to reject or fail to reject your null hypothesis, step 5: present your findings, other interesting articles, frequently asked questions about hypothesis testing. After developing your initial research hypothesis (the prediction that you want to investigate), it is important to restate it as a null (H o ) and alternate (H a ) hypothesis so that you can test it mathematically. The alternate hypothesis is usually your initial hypothesis that predicts a relationship between variables. The null hypothesis is a prediction of no relationship between the variables you are interested in.
Receive feedback on language, structure, and formattingProfessional editors proofread and edit your paper by focusing on:
See an example  For a statistical test to be valid , it is important to perform sampling and collect data in a way that is designed to test your hypothesis. If your data are not representative, then you cannot make statistical inferences about the population you are interested in. There are a variety of statistical tests available, but they are all based on the comparison of within-group variance (how spread out the data is within a category) versus between-group variance (how different the categories are from one another). If the between-group variance is large enough that there is little or no overlap between groups, then your statistical test will reflect that by showing a low p -value . This means it is unlikely that the differences between these groups came about by chance. Alternatively, if there is high within-group variance and low between-group variance, then your statistical test will reflect that with a high p -value. This means it is likely that any difference you measure between groups is due to chance. Your choice of statistical test will be based on the type of variables and the level of measurement of your collected data .
Based on the outcome of your statistical test, you will have to decide whether to reject or fail to reject your null hypothesis. In most cases you will use the p -value generated by your statistical test to guide your decision. And in most cases, your predetermined level of significance for rejecting the null hypothesis will be 0.05 – that is, when there is a less than 5% chance that you would see these results if the null hypothesis were true. In some cases, researchers choose a more conservative level of significance, such as 0.01 (1%). This minimizes the risk of incorrectly rejecting the null hypothesis ( Type I error ). The results of hypothesis testing will be presented in the results and discussion sections of your research paper , dissertation or thesis . In the results section you should give a brief summary of the data and a summary of the results of your statistical test (for example, the estimated difference between group means and associated p -value). In the discussion , you can discuss whether your initial hypothesis was supported by your results or not. In the formal language of hypothesis testing, we talk about rejecting or failing to reject the null hypothesis. You will probably be asked to do this in your statistics assignments. However, when presenting research results in academic papers we rarely talk this way. Instead, we go back to our alternate hypothesis (in this case, the hypothesis that men are on average taller than women) and state whether the result of our test did or did not support the alternate hypothesis. If your null hypothesis was rejected, this result is interpreted as “supported the alternate hypothesis.” These are superficial differences; you can see that they mean the same thing. You might notice that we don’t say that we reject or fail to reject the alternate hypothesis . This is because hypothesis testing is not designed to prove or disprove anything. It is only designed to test whether a pattern we measure could have arisen spuriously, or by chance. If we reject the null hypothesis based on our research (i.e., we find that it is unlikely that the pattern arose by chance), then we can say our test lends support to our hypothesis . But if the pattern does not pass our decision rule, meaning that it could have arisen by chance, then we say the test is inconsistent with our hypothesis . If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.
Methodology
Research bias
Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance. A hypothesis states your predictions about what your research will find. It is a tentative answer to your research question that has not yet been tested. For some research projects, you might have to write several hypotheses that address different aspects of your research question. A hypothesis is not just a guess — it should be based on existing theories and knowledge. It also has to be testable, which means you can support or refute it through scientific research methods (such as experiments, observations and statistical analysis of data). Null and alternative hypotheses are used in statistical hypothesis testing . The null hypothesis of a test always predicts no effect or no relationship between variables, while the alternative hypothesis states your research prediction of an effect or relationship. Cite this Scribbr articleIf you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator. Bevans, R. (2023, June 22). Hypothesis Testing | A Step-by-Step Guide with Easy Examples. Scribbr. Retrieved August 13, 2024, from https://www.scribbr.com/statistics/hypothesis-testing/ Is this article helpful?Rebecca BevansOther students also liked, choosing the right statistical test | types & examples, understanding p values | definition and examples, what is your plagiarism score. An official website of the United States government The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site. The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.
Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .
An Introduction to Statistics: Choosing the Correct Statistical TestPriya ranganathan. 1 Department of Anaesthesiology, Critical Care and Pain, Tata Memorial Centre, Homi Bhabha National Institute, Mumbai, Maharashtra, India The choice of statistical test used for analysis of data from a research study is crucial in interpreting the results of the study. This article gives an overview of the various factors that determine the selection of a statistical test and lists some statistical testsused in common practice. How to cite this article: Ranganathan P. An Introduction to Statistics: Choosing the Correct Statistical Test. Indian J Crit Care Med 2021;25(Suppl 2):S184–S186. In a previous article in this series, we looked at different types of data and ways to summarise them. 1 At the end of the research study, statistical analyses are performed to test the hypothesis and either prove or disprove it. The choice of statistical test needs to be carefully performed since the use of incorrect tests could lead to misleading conclusions. Some key questions help us to decide the type of statistical test to be used for analysis of study data. 2 W hat is the R esearch H ypothesis ?Sometimes, a study may just describe the characteristics of the sample, e.g., a prevalence study. Here, the statistical analysis involves only descriptive statistics . For example, Sridharan et al. aimed to analyze the clinical profile, species distribution, and susceptibility pattern of patients with invasive candidiasis. 3 They used descriptive statistics to express the characteristics of their study sample, including mean (and standard deviation) for normally distributed data, median (with interquartile range) for skewed data, and percentages for categorical data. Studies may be conducted to test a hypothesis and derive inferences from the sample results to the population. This is known as inferential statistics . The goal of inferential statistics may be to assess differences between groups (comparison), establish an association between two variables (correlation), predict one variable from another (regression), or look for agreement between measurements (agreement). Studies may also look at time to a particular event, analyzed using survival analysis. A re the C omparisons M atched (P aired ) or U nmatched (U npaired )?Observations made on the same individual (before–after or comparing two sides of the body) are usually matched or paired . Comparisons made between individuals are usually unpaired or unmatched . Data are considered paired if the values in one set of data are likely to be influenced by the other set (as can happen in before and after readings from the same individual). Examples of paired data include serial measurements of procalcitonin in critically ill patients or comparison of pain relief during sequential administration of different analgesics in a patient with osteoarthritis. W hat are the T ype of D ata B eing M easured ?The test chosen to analyze data will depend on whether the data are categorical (and whether nominal or ordinal) or numerical (and whether skewed or normally distributed). Tests used to analyze normally distributed data are known as parametric tests and have a nonparametric counterpart that is used for data, which is distribution-free. 4 Parametric tests assume that the sample data are normally distributed and have the same characteristics as the population; nonparametric tests make no such assumptions. Parametric tests are more powerful and have a greater ability to pick up differences between groups (where they exist); in contrast, nonparametric tests are less efficient at identifying significant differences. Time-to-event data requires a special type of analysis, known as survival analysis. H ow M any M easurements are B eing C ompared ?The choice of the test differs depending on whether two or more than two measurements are being compared. This includes more than two groups (unmatched data) or more than two measurements in a group (matched data). T ests for C omparison( Table 1 lists the tests commonly used for comparing unpaired data, depending on the number of groups and type of data. As an example, Megahed and colleagues evaluated the role of early bronchoscopy in mechanically ventilated patients with aspiration pneumonitis. 5 Patients were randomized to receive either early bronchoscopy or conventional treatment. Between groups, comparisons were made using the unpaired t test for normally distributed continuous variables, the Mann–Whitney U -test for non-normal continuous variables, and the chi-square test for categorical variables. Chowhan et al. compared the efficacy of left ventricular outflow tract velocity time integral (LVOTVTI) and carotid artery velocity time integral (CAVTI) as predictors of fluid responsiveness in patients with sepsis and septic shock. 6 Patients were divided into three groups— sepsis, septic shock, and controls. Since there were three groups, comparisons of numerical variables were done using analysis of variance (for normally distributed data) or Kruskal–Wallis test (for skewed data). Tests for comparison of unpaired data
A common error is to use multiple unpaired t -tests for comparing more than two groups; i.e., for a study with three treatment groups A, B, and C, it would be incorrect to run unpaired t -tests for group A vs B, B vs C, and C vs A. The correct technique of analysis is to run ANOVA and use post hoc tests (if ANOVA yields a significant result) to determine which group is different from the others. ( Table 2 lists the tests commonly used for comparing paired data, depending on the number of groups and type of data. As discussed above, it would be incorrect to use multiple paired t -tests to compare more than two measurements within a group. In the study by Chowhan, each parameter (LVOTVTI and CAVTI) was measured in the supine position and following passive leg raise. These represented paired readings from the same individual and comparison of prereading and postreading was performed using the paired t -test. 6 Verma et al. evaluated the role of physiotherapy on oxygen requirements and physiological parameters in patients with COVID-19. 7 Each patient had pretreatment and post-treatment data for heart rate and oxygen supplementation recorded on day 1 and day 14. Since data did not follow a normal distribution, they used Wilcoxon's matched pair test to compare the prevalues and postvalues of heart rate (numerical variable). McNemar's test was used to compare the presupplemental and postsupplemental oxygen status expressed as dichotomous data in terms of yes/no. In the study by Megahed, patients had various parameters such as sepsis-related organ failure assessment score, lung injury score, and clinical pulmonary infection score (CPIS) measured at baseline, on day 3 and day 7. 5 Within groups, comparisons were made using repeated measures ANOVA for normally distributed data and Friedman's test for skewed data. Tests for comparison of paired data
T ests for A ssociation between V ariables( Table 3 lists the tests used to determine the association between variables. Correlation determines the strength of the relationship between two variables; regression allows the prediction of one variable from another. Tyagi examined the correlation between ETCO 2 and PaCO 2 in patients with chronic obstructive pulmonary disease with acute exacerbation, who were mechanically ventilated. 8 Since these were normally distributed variables, the linear correlation between ETCO 2 and PaCO 2 was determined by Pearson's correlation coefficient. Parajuli et al. compared the acute physiology and chronic health evaluation II (APACHE II) and acute physiology and chronic health evaluation IV (APACHE IV) scores to predict intensive care unit mortality, both of which were ordinal data. Correlation between APACHE II and APACHE IV score was tested using Spearman's coefficient. 9 A study by Roshan et al. identified risk factors for the development of aspiration pneumonia following rapid sequence intubation. 10 Since the outcome was categorical binary data (aspiration pneumonia— yes/no), they performed a bivariate analysis to derive unadjusted odds ratios, followed by a multivariable logistic regression analysis to calculate adjusted odds ratios for risk factors associated with aspiration pneumonia. Tests for assessing the association between variables
T ests for A greement between M easurements( Table 4 outlines the tests used for assessing agreement between measurements. Gunalan evaluated concordance between the National Healthcare Safety Network surveillance criteria and CPIS for the diagnosis of ventilator-associated pneumonia. 11 Since both the scores are examples of ordinal data, Kappa statistics were calculated to assess the concordance between the two methods. In the previously quoted study by Tyagi, the agreement between ETCO 2 and PaCO 2 (both numerical variables) was represented using the Bland–Altman method. 8 Tests for assessing agreement between measurements
T ests for T ime-to -E vent D ata (S urvival A nalysis )Time-to-event data represent a unique type of data where some participants have not experienced the outcome of interest at the time of analysis. Such participants are considered to be “censored” but are allowed to contribute to the analysis for the period of their follow-up. A detailed discussion on the analysis of time-to-event data is beyond the scope of this article. For analyzing time-to-event data, we use survival analysis (with the Kaplan–Meier method) and compare groups using the log-rank test. The risk of experiencing the event is expressed as a hazard ratio. Cox proportional hazards regression model is used to identify risk factors that are significantly associated with the event. Hasanzadeh evaluated the impact of zinc supplementation on the development of ventilator-associated pneumonia (VAP) in adult mechanically ventilated trauma patients. 12 Survival analysis (Kaplan–Meier technique) was used to calculate the median time to development of VAP after ICU admission. The Cox proportional hazards regression model was used to calculate hazard ratios to identify factors significantly associated with the development of VAP. The choice of statistical test used to analyze research data depends on the study hypothesis, the type of data, the number of measurements, and whether the data are paired or unpaired. Reviews of articles published in medical specialties such as family medicine, cytopathology, and pain have found several errors related to the use of descriptive and inferential statistics. 12 – 15 The statistical technique needs to be carefully chosen and specified in the protocol prior to commencement of the study, to ensure that the conclusions of the study are valid. This article has outlined the principles for selecting a statistical test, along with a list of tests used commonly. Researchers should seek help from statisticians while writing the research study protocol, to formulate the plan for statistical analysis. Priya Ranganathan https://orcid.org/0000-0003-1004-5264 Source of support: Nil Conflict of interest: None R eferences
Statistics By Jim Making statistics intuitive Comparing Hypothesis Tests for Continuous, Binary, and Count DataBy Jim Frost 46 Comments In a previous blog post, I introduced the basic concepts of hypothesis testing and explained the need for performing these tests. In this post, I’ll build on that and compare various types of hypothesis tests that you can use with different types of data, explore some of the options, and explain how to interpret the results. Along the way, I’ll point out important planning considerations, related analyses, and pitfalls to avoid. A hypothesis test uses sample data to assess two mutually exclusive theories about the properties of a population . Hypothesis tests allow you to use a manageable-sized sample from the process to draw inferences about the entire population. I’ll cover common hypothesis tests for three types of variables —continuous, binary, and count data. Recognizing the different types of data is crucial because the type of data determines the hypothesis tests you can perform and, critically, the nature of the conclusions that you can draw. If you collect the wrong data, you might not be able to get the answers that you need. Related posts : Qualitative vs. Quantitative Data , Guide to Data Types and How to Graph Them , Discrete vs. Continuous , and Nominal, Ordinal, Interval, and Ratio Scales Hypothesis Tests for Continuous DataContinuous data can take on any numeric value, and it can be meaningfully divided into smaller increments, including fractional and decimal values. There are an infinite number of possible values between any two values. You often measure a continuous variable on a scale. For example, when you measure height, weight, and temperature, you have continuous data . With continuous variables, you can use hypothesis tests to assess the mean, median, and standard deviation. When you collect continuous data, you usually get more bang for your data buck compared to discrete data. The two key advantages of continuous data are that you can:
I’ll cover two of the more common hypothesis tests that you can use with continuous data—t-tests to assess means and variance tests to evaluate dispersion around the mean. Both of these tests come in one-sample and two-sample versions. One-sample tests allow you to compare your sample estimate to a target value. The two-sample tests let you compare the samples to each other. I’ll cover examples of both types. There is also a group of tests that assess the median rather than the mean. These are known as nonparametric tests and practitioners use them less frequently. However, consider using a nonparametric test if your data are highly skewed and the median better represents the actual center of your data than the mean. Related posts : Nonparametric vs. Parametric Tests and Determining Which Measure of Central Tendency is Best for Your Data Graphing the data for the example scenarioSuppose we have two production methods, and our goal is to determine which one produces a stronger product. To evaluate the two methods, we draw a random sample of 30 products from each production line and measure the strength of each unit. Before performing any analyses, it’s always a good idea to graph the data because it provides an excellent overview. Here is the CSV data file in case you want to follow along: Continuous_Data_Examples .  These histograms suggest that Method 2 produces a higher mean strength while Method 1 produces more consistent strength scores. The higher mean strength is good for our product, but the greater variability might produce more defects. Graphs provide a good picture, but they do not test the data statistically. The differences in the graphs might be caused by random sample error rather than an actual difference between production methods. If the observed differences are due to random error, it would not be surprising if another sample showed different patterns. It can be a costly mistake to base decisions on “results” that vary with each sample. Hypothesis tests factor in random error to improve our chances of making correct decisions. Keep this graph in mind when we look at binary data because they illustrate how much more information continuous data convey. Related posts : Using Histograms to Understand Your Data and How Hypothesis Tests Work: Significance Levels and P-values Two-sample t-test to compare meansThe first thing we want to determine is whether one of the methods produces stronger products. We’ll use a two-sample t-test to determine whether the population means are different. The hypotheses for our 2-sample t-test are:
A p-value less than the significance level indicates that you can reject the null hypothesis. In other words, the sample provides sufficient evidence to conclude that the population means are different. Below is the output for the analysis.  The p-value (0.034) is less than 0.05. From the output, we can see that the difference between the mean of Method 2 (98.39) and Method 1 (95.39) is statistically significant. We can conclude that Method 2 produces a stronger product on average. That sounds great, and it appears that we should use Method 2 to manufacture a stronger product. However, there are other considerations. The t-test tells us that Method 2’s mean strength is greater than Method 1, but it says nothing about the variability of strength values. For that, we need to use another test. Related posts : How T-Tests Work and How to Interpret P-values Correctly and Step-by-Step Instructions for How to Do t-Tests in Excel . 2-Variances test to compare variabilityA production method that has excessive variability creates too many defects. Consequently, we will also assess the standard deviations of both methods. To determine whether either method produces greater variability in the product’s strength, we’ll use the 2 Variances test. The hypotheses for our 2 Variances test are:
A p-value less than the significance level indicates that you can reject the null hypothesis. In other words, the sample provides sufficient evidence for concluding that the population standard deviations are different. The 2-Variances output for our product is below.  Both of the p-values are less than 0.05. The output indicates that the variability of Method 1 is significantly less than Method 2. We can conclude that Method 1 produces a more consistent product. Related post : Measures of Variability What we learned and did not learn with the hypothesis testsThe hypothesis test results confirm the patterns in the graphs. Method 2 produces stronger products on average while Method 1 produces a more consistent product. The statistically significant test results indicate that these results are likely to represent actual differences between the production methods rather than sampling error. Our example also illustrates how you can assess different properties using continuous data, which can point towards different decisions. We might want the stronger products of Method 2 but the greater consistency of Method 1. To navigate this dilemma, we’ll need to use our process knowledge. Finally, it’s crucial to note that the tests produce estimates of population parameters—the population means (μ) and the population standard deviations (σ). While these parameters can help us make decisions, they tell us little about where individual values are likely to fall. In certain circumstances, knowing the proportion of values that fall within specified intervals is crucial. For the examples, the products must fall within spec limits. Even when the mean falls within the spec limit, it’s possible that too many individual items will fall outside the spec limits if the variability is too high. Other types of analysesTo better understand the distribution of individual values rather than the population parameters, use the following analyses: Tolerance intervals : A tolerance interval is a range that likely contains a specific proportion of a population. For our example, we might want to know the range where 99% of the population falls for each production method. We can compare the tolerance interval to our requirements to determine whether there is too much variability. Capability analysis : This type of analysis uses sample data to determine how effectively a process produces output with characteristics that fall within the spec limits. These tools incorporate both the mean and spread of your data to estimate the proportion of defects. Related post : Confidence Intervals vs. Prediction Intervals vs. Tolerance Intervals Proportion Hypothesis Tests for Binary DataLet’s switch gears and move away from continuous data. Suppose we take another random sample of our product from each of the production lines. However, instead of measuring a characteristic, inspectors evaluate each product and either accept or reject it. Binary data can have only two values. If you can place an observation into only two categories, you have a binary variable . For example, pass/fail and accept/reject data are binary. Quality improvement practitioners often use binary data to record defective units. Binary data are useful for calculating proportions or percentages, such as the proportion of defective products in a sample. You simply take the number of defective products and divide by the sample size. Hypothesis tests that assess proportions require binary data and allow you to use sample data to make inferences about the proportions of populations.  2 Proportions test to compare two samplesFor our first example, we will make a decision based on the proportions of defective parts. Our goal is to determine whether the two methods produce different proportions of defective parts. To make this determination, we’ll use the 2 Proportions test. For this test, the hypotheses are as follows:
A p-value less than the significance level indicates that you can reject the null hypothesis. In this case, the sample provides sufficient evidence for concluding that the population proportions are different. The 2 Proportions output for our product is below.  Both p-values are less than 0.05. The output indicates that the difference between the proportion of defective parts for Method 1 (~0.062) and Method 2 (~0.146) is statistically significant. We can conclude that Method 1 produces defective parts less frequently. 1 Proportion test example: comparison to a targetThe 1 Proportion test is also handy because you can compare a sample to a target value. Suppose you receive parts from a supplier who guarantees that less than 3% of all parts they produce are defective. You can use the 1 Proportion test to assess this claim. First, collect a random sample of parts and determine how many are defective. Then, use the 1 Proportion test to compare your sample estimate to the target proportion of 0.03. Because we are interested in detecting only whether the population proportion is greater than 0.03, we’ll use a one-sided test. One-sided tests have greater power to detect differences in one direction, but no ability to detect differences in the other direction. Our one-sided 1 Proportion test has the following hypotheses:
For this test, a significant p-value indicates that the supplier is in trouble! The sample provides sufficient evidence to conclude that the proportion of all parts from the supplier’s process is greater than 0.03 despite their assertions to the contrary. Comparing continuous data to binary dataThink back to the graphs for the continuous data. At a glance, you can see both the central location and spread of the data. If we added spec limits, we could see how many data points are close and far away from them. Is the process centered between the spec limits? Continuous data provide a lot of insight into our processes. Now, compare that to the binary data that we used in the 2 Proportions test. All we learn from that data is the proportion of defects for Method 1 (0.062) and Method 2 (0.146). There is no distribution to analyze, no indication of how close the items are to the specs, and no indication of how they failed the inspection. We only know the two proportions. Additionally, the samples sizes are much larger for the binary data than the continuous data (130 vs. 30). When the difference between proportions is smaller, the required sample sizes can become quite large. Had we used a sample size of 30 like before, we almost certainly would not have detected this difference. In general, binary data provide less information than an equivalent amount of continuous data. If you can collect continuous data, it’s the better route to take! Related post : Estimating a Good Sample Size for Your Study Using Power Analysis Poisson Hypothesis Tests for Count DataCount data can have only non-negative integers (e.g., 0, 1, 2, etc.). In statistics , we often model count data using the Poisson distribution. Poisson data are a count of the presence of a characteristic, result, or activity over a constant amount of time, area, or other length of observation. For example, you can use count data to record the number of defects per item or defective units per batch. With Poisson data, you can assess a rate of occurrence. For this scenario, we’ll assume that we receive shipments of parts from two different suppliers. Each supplier sends the parts in the same sized batch. We need to determine whether one supplier produces fewer defects per batch than the other supplier. To perform this analysis, we’ll randomly sample batches of parts from both suppliers. The inspectors examine all parts in each batch and record the count of defective parts. We’ll randomly sample 30 batches from each supplier. Here is the CSV data file for this example: Count_Data_Example . Performing the Two-Sample Poisson Rate TestWe’ll use the 2-Sample Poisson Rate test. For this test, the hypotheses are as follows:
A p-value less than the significance level indicates that you can reject the null hypothesis because the sample provides sufficient evidence to conclude that the population rates are different. The 2-Sample Poisson Rate output for our product is below.  Both p-values are less than 0.05. The output indicates that the difference between the rate of defects per batch for Supplier 1 (3.56667) and Supplier 2 (5.36667) is statistically significant. We can conclude that Supplier 1 produces defects at a lower rate than Supplier 2. Hypothesis tests are a great tool that allow you to take relatively small samples and draw conclusions about entire populations. There is a selection of tests available, and different options within the tests, which make them useful for a wide variety of situations. To see an alternative approach to these traditional hypothesis testing methods, learn about bootstrapping in statistics ! Share this: Reader InteractionsMay 10, 2024 at 11:06 am Ah that explains why I couldn’t find an R function that returned the same output! Thank you very much for your reply – I can stop looking now! May 9, 2024 at 11:24 am Thank you for this article, I’ve learned a lot from reading it. Your Two-Sample Poisson Rate Test example is very similar in structure to my data so I am trying to follow the same approach. The results pictured look like output from an R function – but I have been unable to find one that outputs results in this way. If these were indeed created by an R library/function, would you mind sharing which one you used, please? Kind regards, Ash May 9, 2024 at 4:49 pm Sorry, I’m not using R. The results are from Minitab statistical software. September 29, 2023 at 3:21 pm Hello guys, what is the outcome varaible in independent sample t test? binary or not? Because it compares the means of two independent populations as which is greater or lower September 29, 2023 at 5:47 pm The outcome variable for an independent sample t-test is continuous because you’re using it to calculate the means for two groups. The binary variable is the categorical factor in the design. The binary variable defines the two groups for which you’re calculating the means. For example, your binary variable could be gender (male/female), experimental group (control/treatment), or material type (A/B). But the outcome variable is continuous so you can calculate the means for both groups and compare them. Click the link to learn more about the test. March 22, 2023 at 3:32 pm The document can’t be found, is the link still working? March 22, 2023 at 3:35 pm You’ll need to specify which link you’re talking about so I can check it. All links should be working. October 9, 2021 at 3:28 am Greetings!!! Very intuitive explanation. Liked the way you have explained with sufficient examples. Jim based on Inferential Statistics, could you include an article on A/B Testing Methodology incorporating from basics like —Data Collection Process, Dataset Splitting Procedures & Duration for carrying out such experiments. Also if you could incorporate illustrations from different industries viz. Healthcare, Manufacturing, Logistics, Quality, Ecommerce, Marketing, Advertisement Domains, this would indeed be useful. Nowadays A/B Testing & Multivariate Testing is being incorporated & implemented in a robust manner across Data Science domain. Article or Write-up regarding this would immensely be useful. Looking forward to a favourable and positive response. August 21, 2021 at 1:22 pm The poisson test example has N of 30. I am wondering the appropriate distribution if the sample is lower than 30. Is it a t statistic or chi-square June 16, 2021 at 12:02 pm Hi, great post! I have an expected and observed data set and want to do additional testing to see if they differ signficantly from each other. Furthermore, the specific entries that contribute to the most weight in that significance or places that should have special attention. I did chi-square goodness of fit, but want to go further. Just to add, this is count data. June 19, 2021 at 4:17 pm I’m not 100% sure what you want to do to go further. Because it’s count data, you could model it with the Poisson or Negative Binomial distribution. If you have other relevant variables, you can fit a Poisson or Negative Binomial regression model to explore relationships in your data. I talk a bit about those types of models in my post about choosing the correct type of regression model . You can also perform hypothesis tests designed for that type of data. The chi-squared test you performed seems like a good one to see how the expected and observed differs! April 29, 2021 at 11:44 pm How do you do a independence test in Stata for a categorical variable with 6 levels and a binary variable. April 30, 2021 at 12:23 am I’m not a Stata user, but it sounds like you need to perform a chi-square test of independence . December 13, 2020 at 1:00 pm Hi Jim – thank you for this great site! I have a situation where there is a reference standard (tells me if there is truly fat in a mass) and I have 2 different methods of detecting if there is (or is not) fat in the mass. My null hypothesis is that there is no difference in detection. I have a set of masses where I know if there is fat in the masses and used the 2 methods to detect whether they were able to detect the fat. Is the 2 proportions test the most appropriate for this question? Thank you so much! December 3, 2020 at 8:31 am Thank you Jim for the wonderful post. It was clearly written and I enjoyed reading through it. I have an additional query. I wanted to compare the variances of two methods of measurement applied at each observation point of a field survey. The variables from both methods have binary data type. How can I do the statistical test. Thank you in advance for your help. December 3, 2020 at 3:02 pm With binary data, you can’t compare variances. You can compare proportions using a proportions test. I discuss these tests in the binary section of this post. To read an example of a 2-sample proportions test, read my post about flu shot effectiveness . In it, I use 2-proportions tests to evaluate real flu study data. Or read my post about Mythbusters test about whether yawns are contagious , where I use a 2-proportions test. That way you can see what these tests can do. I cover them, and many other tests, in much more detail in my Hypothesis Testing book ! I hope this helps! August 5, 2020 at 9:36 pm Hi Jim. Just wanted to follow up and see if you’ve had a chance to review this question yet? August 6, 2020 at 1:09 am Hi Jack, thanks for the reminder! I just replied! August 3, 2020 at 4:45 am Hi Jim , a green belt has a project on flu vaccinations , with 5 data points, % vaccination rates per year averaging about 36% of staff numbers. Her project was to increase vaccination rates this year , and has accumulated a lot of data points to measure vaccination rates in different office areas as a percent of total staff numbers which have almost doubled. Should she use 2 sample t test to measure difference in means between before and after data ( continuous) or should she use 2 sample test for proportions (attribute). There is small sample size for before data and large sample size for after data August 5, 2020 at 12:46 am I see two possibilities. The choice depends on whether she measured the same sites in the before and after. If they’re different sites before and after, she has independent groups and can use the regular 2-sample proportions test. If they’re the same sites before and after, she can use either the test of marginal homogeneity or McNemar’s test. I have not used these tests myself and cannot provide more information. However, if she used the same sites before and after, she has proportions data for dependent groups (same groups) and should not use the regular 2-sample proportions test. These two tests can handle proportions for dependent groups. July 19, 2020 at 3:18 am Hi Jim. Would I be able to use the 2 Proportion Test for comparing 2 proportions from different time periods? Example scenario: I run a satisfaction survey on a MOOC site during Q1 to a random sample of visitors and find that 80% of them were satisfied with their experience. The following quarter I run the same survey and find that 75% were satisfied. Is the 5 percentage point drop statistically significant or just due to random noise? Sorry about the delay in replying! Sometimes comments slip through the cracks! Yes, you can do as you suggest assuming the respondents are different in the two quarters and assuming that the data are binary (satisfied/not satisfied). The 2 proportions test is designed for independent groups and binary data. I hope that helps even belatedly! May 19, 2020 at 9:58 pm Thanks…Let me see that document May 19, 2020 at 7:04 pm I would like to ask about 2 sample poisson rate. How do you calculate the 95% CI and test for difference ? Your answer is really appreciated. Thank you so much for giving this tutorial. May 19, 2020 at 9:17 pm This document describes the calculations. I hope it helps! March 6, 2020 at 4:52 am Thank you so much for your kind support. Esteemed regards. March 5, 2020 at 9:23 pm Thanks for your helpful comments. Basically I have developed my research model based on competing theories. For example, I have one IV (Exploitation) and Two DV’s (Incremental innovation and Radical Innovation). Each variable in the model has own indicators. Some researchers claims that exploitation support only incremental innovations. On the other hand there are also studies that claims that in-depth exploitation also support radical innovation. However, these researchers claim that exploitation support radical innovations in a limited capacity as compared to incremental innovation. ON the basis of these competing theories I developed my hypothesis as: Exploitation significantly and positively influences both incremental and radical innovation, however exploitation influence incremental innovation more than radical innovation. Thank you very much for your quick response. Its really helpful. March 6, 2020 at 1:46 am Hi Shabahat, Thanks you for the additional information. I messed up one thing in my previous reply to you. Because you only have the one IV, you don’t need to worry about standardizing that IV for comparability. However, assuming the DVs use different units of measurement, that’ll make comparisons problematic. Consequently, you probably need to standardize the two dependent variables instead. You’d learn how a one unit change in the IV relates to the standard deviation of each DV. That puts the DVs on the same scale. See how other researchers have handled this situation in your field to be sure that’s an accepted approach. Additionally, if you find a significant relationship between exploitation and radical innovation, then you’d have good evidence to support that claim you’re making. March 5, 2020 at 2:37 am Hi Jim, Its really amazing. However I have a query regarding my analysis. I have one independent variable (Continuous) and Two dependent variables (Continuous). In the linear regression, the Independent variable significantly explains both dependent variables. Problem: Now i want to compare the effect of my Independent variable on both dependent variables. How can I compare?. If the effect is different, how can I test whether the effect difference is statistically significant or not in SPSS. March 5, 2020 at 4:01 pm The fact that you’re talking about different DVs complicates things because they’re presumably measuring different things and using different units, which makes comparison difficult. The standardized coefficients can help you get around that but it changes the interpretation of the results. Assuming that the two DV variables measure different characteristics, you might try standardizing your IVs and fitting the model using the standardized values. This process produces standardized coefficients, which use the same units and allows you to compare–although it does change the interpretation of the coefficients. I write about this in my post about assessing the importance of your predictors . You can also look at the CIs for the standardized coefficients and see if they overlap. If they don’t overlap, you know the difference between the standardized coefficients is statistically significant. January 20, 2019 at 12:40 pm Great Post! Can we test proportions from a continuos variable with unknown distribution using the poisson distribution using a cut-off value for good and bad samples and couting them? November 14, 2018 at 4:05 pm Hi Jim, I really enjoy reading your posts and they have cleared many stat concepts! I had a question about the chi square probability distribution. Although it is a non-parametric test, why does it fall into a continuous probability distribution and why can we use the chi square distribution for categorical data if it’s a continuous probability distribution? November 14, 2018 at 10:53 pm Hi Sanjana, That’s a great question! I’m glad you’re thinking about the types of variables and distributions, and how they’re used together. You’re correct on both counts. Chi-squared test of independent is nonparameteric because it doesn’t assume a particular data distribution. Additionally, analysts use it to test the independence of categorical variables . There are other ways to use this distribution as well. Now, onto why we use chi-square (a distribution for continuous data) with categorical variables! Yes, it involves categorical variables, but the analysis assesses the observed and expected counts of these variables. For each cell, the analysis takes the squared difference between the observed count and the expected count and then divides that by the expected count. These values are summed acrossed all cells to produce the chi-square value. This process produces a continuous variable that is based on the differences between the observed and expected counts of the categorical variables. When the value of this variable is large enough, we know that the difference between the observed counts and the expected counts is large enough to be unlikely due to chance. And, that’s why we use a continuous distribution to analyze categorical variables. May 27, 2018 at 12:58 am This is very helpful! Thank you! May 26, 2018 at 11:38 pm Hi Jim, Great post. I was wondering, do you know of any references that discuss the difference in sample size between binary and continuous data? I am looking for a reference to cite in a journal article. Thanks, Amanda. May 26, 2018 at 11:55 pm The article I cite below discusses the different sample sizes in terms of observations per model term in order to avoid overfitting your model. I also cover these ideas in my post about how to avoid overfitting regression models . For regression models, this provides a good context for sample size requirements. Babyak, MA., What You See May Not Be What You Get: A Brief, Nontechnical Introduction to Overfitting in Regression-Type Models, Psychosomatic Medicine 66:411-421 (2004). February 3, 2018 at 7:04 am I am totally new to statistics, Following a small sample from my dataset. Views PosEmo NegEmo 1650077 2.63 1.27 753826 2.39 0.47 926647 1.71 1.02 Views = Dependent continous Variable PosEmo = Independent Continous Variable NegEmo = Independent Continous Variable My query : 1. How to run Hypothesis testing on same, Im pretty confused what to use , what to do , I am using SPSS modeler and SPSS statistics tool. 2.I think Multiple Regression is Ok for this . Let me know how to use it in SPSS modeler or stats tool. Regards Sarika February 5, 2018 at 1:30 am Hi Sarika, yes, it sounds like you can use multiple regression for those data. The hypothesis test in this case would be the p-values for the regression coefficients . Click that link to learn more about that. In your stats software, choose multiple linear regression and then specify the dependent variable and the two independent variables. Fit the model and then check the statistical output and the residual plots to see if you have a good model. Be sure to check out my regression tutorial too. That covers many aspects of regression analysis. November 30, 2017 at 8:45 pm Thanks for your sharing! In the binary case (or proportion case), is there any comparison between “two proportion test” and “Chi-square” test? Is there any guideline to choose which test to use? November 30, 2017 at 9:46 pm You’re welcome! Regarding your question, a two proportion test requires one categorical variable with two levels. For example, the variable could be “test result” and the two levels are “pass” and “fail.” A chi-square test of independence requires at least two categorical variables. Those variables can have two or more levels. You can read an example of the chi-square test of independence that I’ve written about. The example is based on the original Star Trek TV series and determines whether the uniform color affects the fatality rate. That analysis has two categorical variables–fatalities and uniform color. Fatalities has two levels that indicate whether a crewmember survived or died. Uniform color has three levels–gold, blue, and red. As you can see, the data requirements for the two tests are different. I hope this helps! Jim November 30, 2017 at 2:18 am November 29, 2017 at 10:41 pm Great post. Thanks for sharing your expertise. November 29, 2017 at 11:38 pm Thank you! I’m glad it was helpful. November 29, 2017 at 9:02 pm Very nice article. Could you explain more on hypothesis testing on median? November 29, 2017 at 11:39 pm Thank you! For more information about testing the median, click the link in the article for where I compare parametric vs nonparametric analyses. November 29, 2017 at 6:51 pm Please let me know when one can use Probit Analysis. May I know the Procedure in SPSS. Comments and Questions Cancel reply
December 15 Ordinal Data – What Is It, And How Do You Analyse It?Blog, Discover Data 0 comments Ordinal data is one of only 4 types of data in statistics. Do you know what they all are and what you can do with them? If you want to know everything there is to know about Ordinal data - definitions, examples, analysis and statistics - then you're in the right place. When you're done here, you'll also want to read this post's sister articles on quantitative data and qualitative data , Nominal data , Interval data and Ratio data . For now, though, here is our guide to Ordinal data and how to deal with them... Disclosure: we may earn an affiliate commission for purchases you make when using the links to products on this page. As an Amazon Affiliate we earn from qualifying purchases. This post forms part of a series on the 4 types of data in statistics. For more detail, choose from the options below: 4 Types of Data in Statistics: IntroductionNominal data, ordinal data, interval data, all 4 types of data compared, statistical hypothesis testing, what is ordinal data. If you want a simple definition of Nominal data, it would be this: Ordinal Data Definition Ordinal data is a type of categorical data in which the values follow a natural order Ordinal data is the statistical data type that has the following characteristics: 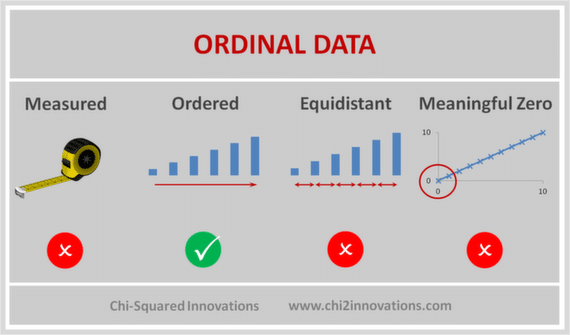 Ordinal Data are observed, not measured, are ordered but non-equidistant and have no meaningful zero Their categories can be ordered (1st, 2nd, 3rd, etc. - hence the name 'ordinal'), but there is no consistency in the relative distances between adjacent categories. As with Nominal data, Ordinal data can have 2 categories, and we also call these dichotomous data. The only difference between Nominal dichotomous data and Ordinal dichotomous data is that Ordinal dichotomous data have an order, whereas Nominal dichotomous data do not.  Pin it for laterNeed to save this for later? Pin it to your favourite board and you can get back to it when you're ready. Ordinal Data ExamplesExamples of Ordinal data include:
In the examples of Ordinal data above, there is an obvious order to the categories. Are any of the examples of Ordinal data above examples of dichotomous data? 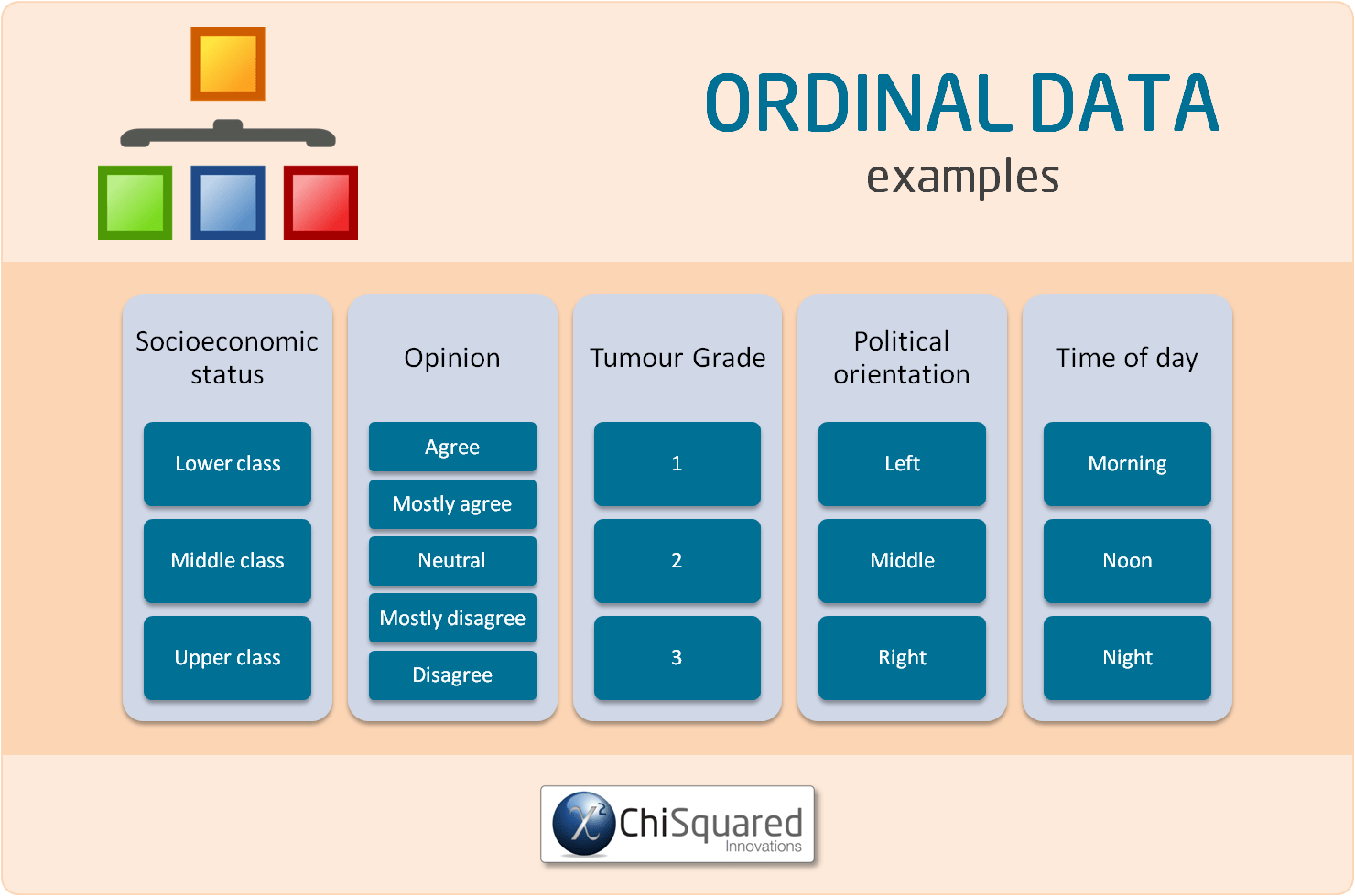 What Can You Calculate With Ordinal Variables?When Ordinal data are used in analysis, they are called Ordinal Variables, so that's what we'll call them from here. With Ordinal variables you can group the data by assessing whether they are the same or different. As Ordinal variables are ordered, they can be sorted by making simple comparisons between the categories, such as Greater/Less than , M ore / Less , Higher/Lower , etc.. You can't do any mathematical operations with Ordinal variables, though, because they aren't numerical data.  For example, you can group people according to their socioeconomic status, but you can also sort them as well. Upper class is higher on the scale than Middle class, which in turn is higher than Lower class. 3 Simple Questions...What's Stopping You Reaching YOUR Data Ninja Potential? Answer 3 questions and we'll recommend the best route to super-charge your data career What Descriptive Statistics Can You Do With Ordinal Data?With Ordinal variables you can calculate precisely the same things as you can with Nominal variables, with a couple of extra things (see if you can spot them). That is:
Learn More About Statistics and Data with These Books:What data visualisations can you do with ordinal variables. As with Nominal variables, since the only descriptive statistics you can do with Ordinal data are frequencies, proportions and percentages, the only ways to visualise these are with pie charts and bar charts.  Ordinal Data Also Make Great Dummy Variables!By now you might be wondering whether you can create dummy variables with Ordinal data. Well, you can! It can be slightly different with Ordinal data, though, because their categories are ordered. Instead of choosing a category, you would usually use a cut-off value and base your dummy variable around that. Let's look at an example. Say you have ages categorised as 20's, 30's, 40's, 50's and 60's, and you suspect that your data are different for those 50 and above. Here, you would code all ages below 50 as 0 and all ages 50+ as 1. You now have a dummy variable, and you can analyse it using all the same techniques as you would a dummy variable created using Nominal data. Ordinal variables are very common in surveys and questionnaires, and the Likert scale is one example of collecting Ordinal data. You can use Ordinal variables in non-parametric hypothesis tests that rely on ranking, such as the Mann-Whitney U-test or the Wilcoxon Matched-Pairs test. Ordinal Data - What Is It, And How Do You Analyse It? Everything You Need To Know (And More) @chi2innovations #dataanalytics #datatypes #statistics What Statistics Can You Do With Ordinal Variables?Ordinal variables can be used in precisely the same statistical hypothesis tests as Nominal variables. Actually, that's not quite true - there are some additional tests you can use with Ordinal variables, but they are more advanced and are beyond the scope of this article. If you want to know more, you can look up the Chi-Squared For Trend Test, Ordinal Logistic Regression and Nominal Logistic Regression. For now, just know that for the pairwise tests, you can treat Ordinal variables and Nominal variables exactly the same.  Ordinal vs Nominal Data - What is the Difference?Ordinal data and Nominal data are both qualitative data, and the difference between them is that Nominal data can only be classified - arranged into classes or categories - whereas Ordinal data can be classified and ordered. One of the assumptions of Ordinal data is that although the categories are ordered, they do not have equal intervals. It is interesting to note that in practice some Ordinal data are treated as though they do have equal intervals because the statistical tests that can be used on these data are much more powerful than those typically used on Ordinal data. This is OK as long as your data collection methods ensure that the equidistant rule isn't bent too much. Tumour Grade [1, 2, 3] is a classic example of this in healthcare.  UNIQUE VIDEO COURSEIn less than 2 hours your data can be:
Ordinal Data: SummaryThe basics of statistics, like data collection , data cleaning and data integrity aren't sexy, and as a result are often neglected, and that is also the case with data types. In my experience, few people that have to do statistics as part of their research know and understand the statistical data types, and as a result struggle to get to grips with what they can and can't do with their data. That's a shame, because as you've seen, if you know the 4 types of data in statistics you know:
In short, data types are a roadmap to doing your entire study properly. They really are that important! Hopefully, by now you have a good understanding of what Ordinal data are, and what you can do with them. Ordinal Data are observed, not measured. They are ordered but non-equidistant and have no meaningful zero. Categories are named, and once data are grouped you can sort them. Ordinal data are types of Qualitative data (also known as categorical data), and you cannot perform any mathematical operations on Ordinal data. Now that you know everything there is to know about Ordinal data, you might also like to read this post's sister articles on quantitative data and qualitative data , Nominal data , Interval data and Ratio data . In the final posts we'll compare each of the 4 types of data and I'll also show you how to choose the correct statistical hypothesis test . Do you have any questions about Ordinal data? Is there something that I've missed out? Let me know in the comments below - your feedback will help me to improve the post and make learning about data and statistics easier for everybody!  data tips, ordinal data, qualitative data You may also like45+ awesome gifts for data scientists, statisticians and other geeks, computational statistics is the new holy grail – experts, 3 crucial tips for data processing and analysis, correlation is not causation – pirates prove it, cracking chi-square tests: step-by-step, chi-square test: the key to categorical analysis, types of data in statistics, free booklet. Download your FREE Booklet and learn how to deal with Statistical Data Types - all of them!  types of Data in StatisticsFree booklet. Have you ever looked at your data and wondered how and where to get started? If you don't know the difference between Quantitative and Qualitative data, or between Ratio, Interval, Ordinal, and Nominal data, then you're in the right place. Here is our guide to statistical data types and how to deal with them.   Five Ways to Analyze Ordinal Variables (Some Better than Others)by Karen Grace-Martin 6 Comments  But that doesn’t mean that you’re stuck with few options. There are more than you’d think. Some are better than others, but it depends on the situation and research questions. Here are five options when your dependent variable is ordinal. 1. Analyze ordinal variables as if they’re nominalOrdinal variables are fundamentally categorical. One simple option is to ignore the order in the variable’s categories and treat it as nominal . There are many options for analyzing categorical variables that have no order. This can make a lot of sense for some variables. For example, when there are few categories and the order isn’t central to the research question. The biggest advantage to this approach is you won’t violate any assumptions . 2. Analyze ordinal variables as if they’re numericBecause the ordering of the categories often is central to the research question, many data analysts do the opposite: ignore the fact that the ordinal variable really isn’t numerical and treat the numerals that designate each category as actual numbers. This approach requires the assumption that the distance between each set of subsequent categories is equal. And that can be very difficult to justify. So think long and hard about whether you’re able to justify this assumption. 3. Non-parametric testsSome good news: there are other options. Many non-parametric descriptive statistics are based on ranking numerical values. Ranks are themselves ordinal–they tell you information about the order, but no distance between values. Just like other ordinal variables. So while we think of these tests as useful for numerical data that are non-normal or have outliers, they work for ordinal variables as well, especially when there are more than just a few ordered categories. Common rank-based non-parametric tests include Kruskal-Wallis , Spearman correlation , Wilcoxon-Mann-Whitney, and Friedman. Each test has a specific test statistic based on those ranks, depending on whether the test is comparing groups or measuring an association. The limitation of these tests, though, is they’re pretty basic. Sure, you can compare groups one-way ANOVA style or measure a correlation, but you can’t go beyond that. You can’t, for example, include interactions among two independent variables or include covariates. You need a real model to do that. 4. Ordinal logistic & probit regressionThere aren’t many tests that are set up just for ordinal variables, but there are a few. One of the most commonly used is ordinal models for logistic (or probit ) regression. There are a few different ways of specifying the logit link function so that it preserves the ordering in the dependent variable. The most commonly available in software is the cumulative link function, which allows you to measure the effect of predictors on the odds of moving into any next-highest-ordered category. These models are complex, have their own assumptions, and can take some practice to interpret. But they are also sometimes exactly what you need. They are a very good tool to have in your statistical toolbox. 5. Rank transformationsAnother model-based approach combines the advantages of ordinal logistic regression and the simplicity of rank-based non-parametrics. The basic idea is a rank transformation: transform each ordinal outcome score into the rank of that score and run your regression, two-way ANOVA, or other model on those ranks. The thing to remember though, is that all results need to be interpreted in terms of the ranks. Just as a log transformation on a dependent variable puts all the means and coefficients on a log(DV) scale, the rank transformation puts everything on a rank scale. Your interpretations are going to be about mean ranks, not means.  Reader InteractionsJune 26, 2024 at 7:39 am How ordinal data can be analyzed by mean? June 26, 2024 at 9:08 am Well, you have to make some really big assumptions to do it. December 4, 2022 at 5:32 am What’s the inferential statistical techniques for all the level of measurement in statistics October 21, 2022 at 8:12 pm For #5, it has been shown that interaction effects under simple rank transformations explode Type I error rates. Put simply, you can’t just rank-transform your DV and run, say, a two-way ANOVA and safely interpret the interaction effect. An increasingly common fix is to use the ALIGNED rank transform (ART), which aligns the response for each main effect and interaction separately, before ranking. This procedure preserves correct Type I error rates for all effects, including interactions. We created an R package called ARTool that performs the ART procedure and gives ANOVA table results. We also have a Windows executable for aligning-and-ranking data. You can find out more on our project page here: http://depts.washington.edu/acelab/proj/art/ October 26, 2022 at 9:58 am Thanks, Jacob. I’ll take a look. I hadn’t heard of aligned rank transformation. October 14, 2020 at 9:17 am 1. am running ordinal logistic regression in stata but when I tried parallel lines test using the command oparallel it responded me in some explanatory variables as hessian is not negative semi definite and in some it says full model can’t be estimated due to perfect prediction. how can I solve this problem, please? 2. I have two categorical variables which are ordinal, what is the best way to analyze my data either using ordinal logistic regression for each of the dependent variable or any one model to use in combination? sincerely! Leave a Reply Cancel replyYour email address will not be published. Required fields are marked * Privacy OverviewOrdinal Scale and Nonparametric Methods As ordinal scales are frequently encountered in research studies, the usual parametric tests don't hold true because of two reasons. First, they assume a level of measurement of interval/ratio scales. Second, they assume that the samples are drawn from a population with a known distribution such as the normal distribution. Measurement of attitudes, consumer tastes and preferences, and ranking of attributes are very prevalent in research. You need exclusive hypothesis testing procedures that deal with ordinal scales. These fall under a set of elegant nonparametric methods. This article attempts to give an illustrative account of nonparametric methods that are used in ordinal scales of measurement. The coverage is by no means exhaustive. However typical situations are discussed to throw light on how useful these tests are. Next-Kolmogorov-Smirnov Test Kolmogorov-Smirnov Test: Kolmogorov-Smirnov test is a test of goodness of fit for the univariate case when the scale of measurement is ordinal. It is similar to the chi-square test of goodness of fit in the sense it also examines whether the observed frequencies are in accordance with the expected frequencies under a well defined null hypothesis. Of course the chi-square test involves nominal measurement. Kolmogorov-Smirnov test is more powerful than the chi-square test when ordinal data are encountered in any decision problem. In the concluding remarks, you will see the advantages of using Kolmogorov-Smirnov test over the chi-square test. To understand how this test works in practice, let us take an example. A manufacturing company producing decorative paints is interested in knowing whether the consumers have distinct preferences for different shades in the context of a new decorative paint that it proposes to market. If the consumers have special preference for any particular shade, then the company would market only that shade. Else, it would plan to market all the shades. A sample of 150 consumers was interviewed and the data collected on shade preferences are given in the table below: Table showing shade preferences
What are your conclusions? Next-Analysis and Interpretations previous Analysis and Interpretations: The test involves comparing the expected cumulative distribution function under the null hypothesis being true with that of observed cumulative distribution function. If we designate Fo(X) as the expected cumulative distribution function and Sn(X) as the observed cumulative distribution function, Kolmogorov-Smirnov D is calculated as D = Max |Fo(X)-Sn(X)| (D is the absolute difference between the expected cumulative proportion and the observed cumulative proportion). Please note that n is the sample size. The following table shows the necessary calculations. Table1: Basic Calculations for the Example
The null hypothesis is that all shades are equally preferred The alternative hypothesis is that they are not equally preferred Computed D = Max |Fo(X)-Sn(X)| = 0.1667. The critical D value for a level of significance of 5% is given by
Next- Concluding Remarks on Kolmogorov-Smirnov Test previous Concluding Remarks on Kolmogorov-Smirnov Test You could very well have used the chi-square test of goodness of fit for testing the hypothesis of equal preference for all shades in this example instead of the Kolmogorov-Smirnov test. When the data measurement are ordinal, Kolmogorov-Smirnov test is more powerful than the chi-square test for the following reasons. Median Test Median Test: Median test is used for testing whether two groups differ in their median value. In simple terms, median test will focus on whether the two groups come from populations with the same median. This test stipulates the measurement scale is at least ordinal and the samples are independent (not necessary of the same sample size). The null hypothesis structured is that the two populations have the same median. Let us take an example to appreciate how this test is useful in a typical practical situation. Example: A private bank is interested in finding out whether the customers belonging to two groups differ in their satisfaction level. The two groups are customers belonging to current account holders and savings account holders. A random sample of 20 customers of each category was interviewed regarding their perceptions of the bank's service quality using a Likert-type (ordinal scale) statements. A score of "1" represents very dissatisfied and a score of "5" represents very satisfied. The compiled aggregate scores for each respondent in each groupare tabulated be given below:
What are your conclusions regarding the satisfaction level of these two groups? Next-Analysis and Interpretations previous The first task in the median test is to obtain the grand median. Arrange the combined data of both the groups in the descending order of magnitude. That is rank them from the highest to the lowest. Select the middle most observation in the ranked data. In this case, median is the average of 20th and 21st observation in the array that has been arranged in the descending order of magnitude. Table showing descending order of aggregate score and rank in the combined sample
Grand median is the average of 20th and 21st observation = (62+61)/2 =61.5. Please note that in the above table, average rank is taken whenever the scores are tied. The next step is to prepare a contingency table of two rows and two columns. The cells represent the number of observations that are above and below the grand median in each group. Whenever some observations in each group coincide with the median value, the accepted practice is to first count the observations that are strictly above grand median and put the rest under below grand median. In other words, below grand median in such cases would include less than or equal to grand median. Scores of Current Account Holders and Savings Account Holders as compared with Grand Median
Null Hypothesis: There is no difference between the current account holders and savings account holders in the perceived satisfaction level. alternative Hypothesis: There is difference between the current account holders and savings account holders in the perceived satisfaction level. The test statistic to be used is given by
on substituting the values of a, b, c, d, and n we have Critical chi-square for 1 d.f at 5% level of significance = 3.84. Since the computed chi-square(0.90) is less than critical chi-square(3.84), we have no convincing evidence to reject the null hypothesis. Thus the the data are consistent with the null hypothesis that there is no difference between the current account holders and savings account holders in the perceived satisfaction level. Home Ordinal DataA type of data in which the data values follow a natural order What is Ordinal Data?In statistics, ordinal data are the type of data in which the values follow a natural order. One of the most notable features of ordinal data is that the differences between the data values cannot be determined or are meaningless. Generally, the data categories lack the width representing the equal increments of the underlying attribute.  In some cases, the values of interval or ratio data can be grouped together to obtain the data’s characteristics. For example, the ranges of income are considered ordinal data while the income itself is the ratio data. Unlike interval or ratio data, ordinal data cannot be manipulated using mathematical operators. Due to this reason, the only available measure of central tendency for datasets that contain ordinal data is the median. Uses of Ordinal DataOrdinal data are commonly employed in various surveys and questionnaires. The Likert scale that you may find in many surveys is one example. The Likert scale lists the categories of the psychometric scale such as “Strongly Agree,” “Agree,” etc. Various examples of this data type can be frequently encountered in finance and economics. Consider an economic report that investigates the GDP levels of different countries. If the report ranks the countries according to their GDP figures, the ranks are examples of ordinal data. How to Analyze the Data?The simplest way to analyze ordinal data is to use visualization tools . For instance, the data may be presented in a table in which each row indicates a distinct category. In addition, they can also be visualized using various charts. The most commonly used chart for representing such types of data is the bar chart. Ordinal data can also be analyzed using advanced statistical analysis tools such as hypothesis testing . Note that the standard parametric methods such as t-test or ANOVA cannot be applied to such types of data. The hypothesis testing of the data can be carried out only using nonparametric tests such as the Mann-Whitney U test or Wilcoxon Matched-Pairs test. More ResourcesTo keep learning and developing your knowledge of financial analysis, we highly recommend the additional CFI resources below:
 Create a free account to unlock this TemplateAccess and download collection of free Templates to help power your productivity and performance. Already have an account? Log in Supercharge your skills with Premium TemplatesTake your learning and productivity to the next level with our Premium Templates. Upgrading to a paid membership gives you access to our extensive collection of plug-and-play Templates designed to power your performance—as well as CFI's full course catalog and accredited Certification Programs. Already have a Self-Study or Full-Immersion membership? Log in Access Exclusive TemplatesGain unlimited access to more than 250 productivity Templates, CFI's full course catalog and accredited Certification Programs, hundreds of resources, expert reviews and support, the chance to work with real-world finance and research tools, and more. Already have a Full-Immersion membership? Log in An official website of the United States government The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site. The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.
Save citation to fileEmail citation, add to collections.
Add to My BibliographyYour saved search, create a file for external citation management software, your rss feed.
Hypothesis testing and estimation in ordinal data under a simple crossover designAffiliation.
Since each patient serves as his/her own control, the crossover design can be of use to improve power as compared with the parallel-groups design in studying noncurative treatments to certain chronic diseases. Although the research studies on the crossover design have been quite intensive, the discussions on analyzing ordinal data under such a design are truly limited. We propose using the generalized odds ratio (GOR) for paired sample data to measure the relative effect on patient responses for both treatment and period in ordinal data under a simple crossover trial. Assuming the treatment and period effects are multiplicative, we note that one can easily derive the maximum likelihood estimator (LE) in closed forms for the GOR of treatment and period effects. We develop asymptotic and exact procedures for testing treatment and period effects. We further derive asymptotic and exact interval estimators for the GOR of treatment and period effects. We use the data taken from a crossover trial to assess the clarity of leaflet instructions between two devices among asthma patients to illustrate the use of these test procedures and estimators developed here. PubMed Disclaimer Similar articles
LinkOut - more resourcesFull text sources.
NCBI Literature Resources MeSH PMC Bookshelf Disclaimer The PubMed wordmark and PubMed logo are registered trademarks of the U.S. Department of Health and Human Services (HHS). Unauthorized use of these marks is strictly prohibited.
Follow along with the video below to see how to install our site as a web app on your home screen. Note: This feature may not be available in some browsers.
Hypothesis test on ordinal data
A PF MountainYou can; with caveats. Try googling chi-square test ( http://en.wikipedia.org/wiki/Chi-square_test ) I could do proportions and use test statistic for proportions but the neutral category causes problem because that splits the customer base into categories. -Satisfied -Neutral -Dissatisfied. You could use binary variables: Is the customer highly satisfied? Is the customer at least satisfied? Is the customer at least neutral? Is the customer at least dissatisfied? ultimatejester said: Thank you for replying(much sooner than i expected :) I am familiar with chi distribution but i don't think it would work here
hey this may sound weird but i have the same question well it seems the same.. and I am stuck I am just wondering how you did it? did u use the population proportion? Yes, i used proportions. You can change the code for success from 1,2,3,4,5 but the one you are really interested in is the "highly satisfied" or 1. I did a one tail test since the company wants to know where its is meeting the required 95% level. To get you started H0: u=95% H1: U<95% Good Luck satisfaction question so would you recommend using the t-test, since the std. dev. is unknown? also, wat would the null and alternative hypotheses be? thanks a lot!
The null and alternative hypothesis are mentioned in my above post. You can't use the t-test. All you are allowed to do on data in count the occurences. Use proportions. Post here if you need more help. Thanks. Adil.A
Hi, I was wondering if u could post how u did that question. I'm having the same problem and i still can't figure it out :( Any help would be really appreciated! Thanks! Dona. Related to Hypothesis test on ordinal dataA hypothesis test on ordinal data is a statistical analysis that is used to determine whether there is a significant difference between two or more groups on an ordinal scale. It is commonly used in social sciences and other fields where data is ranked in a specific order. A hypothesis test on ordinal data is different from other types of hypothesis tests because it uses data that is ranked in a specific order instead of numerical values. This type of test also uses non-parametric statistical methods, which do not assume a normal distribution of the data. Ordinal data can include things like rankings, ratings, and categories such as "strongly agree", "agree", "neutral", "disagree", and "strongly disagree". It can also include data that is in a specific order, such as education level (e.g. high school, college, graduate school). The steps involved in conducting a hypothesis test on ordinal data include: 1) defining the research question and hypothesis, 2) selecting an appropriate statistical test, 3) collecting and organizing the data, 4) performing the statistical test, 5) interpreting the results, and 6) drawing conclusions and making recommendations based on the results. One limitation of hypothesis tests on ordinal data is that they do not provide information about the size or magnitude of the difference between groups. They also cannot determine causation, only association. Additionally, the results of these tests may be affected by the way the data is ranked or categorized. Similar threads
Hot Threads
Recent Insights
Stack Exchange NetworkStack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers. Q&A for work Connect and share knowledge within a single location that is structured and easy to search. Test on Ordinal data with intervalI have a query regarding statistical analysis. I have collected data on percentage of savings done by individuals. These data are ordinal, grouped into equal intervals with the exception of the final category representing all savings of 50% or higher. Because of this, I gather I can't apply a parametric test. I want to study whether there is significant difference in saving habits of two groups. Please suggest an appropriate test. I have a screen shot of the data. Would a t-test or Mann Whitney U-test be appropriate? 
2 Answers 2When the intervals are equally spaced, the data are perhaps ordinal by name only. The T-test summarizes the actual mean difference in % savings. Alas, the largest threshold group is not equal in spacing to the prior groups. So you must reframe the question slightly. If a non-parametric test is a consideration, then perhaps you are less interested in quantifying the actual % difference between men and women. In that case, you could use the T-test anyway and comment on the statistical significance as suggesting whether one group saves more or less than the other. This "non-parametric T test" is asymptotically equivalent to the Mann-Whitney test. Another approach is to use ordinal logistic regression. This is also called a proportional odds model. Expand the data using a full data matrix of 252+98 observations or use a weighted dataset for the 10 tabular values: Then fit the model with Savings as a response, sex as the main predictor, and supply the Weight to obtain a semi-parametric test of statistical significance. Lastly, you are not forbidden from using a parametric model. Simply declare an underlying parametric model for the distribution of savings, and use expectation-maximization to estimate the latent beta (or other appropriate) distribution of savings in males and in females, then estimate the T-test of association. Following up on the response by @AdamO, in my experience with this kind of data, a Wilcoxon-Mann-Whitney test usually corresponds to ordinal regression pretty well. I have some plots on this question near the bottom of this webpage . As always, it's best not to put too much emphasis on the p -value, but to also assess the size of the effect. Looking at the proportions in each category for each sex, it's clear that Male has a higher proportion in "below 10%" than does Female, and that Female has higher proportions in some of the higher categories. But the overall size of the differences is relatively small: Vargha and Delaney's A suggests that the probability of Female having a higher observation than Male is only 0.57 (95% confidence interval, 0.502, 0.629, not shown below). Whether this effect size has practical importance is up to you. For this data in R:  Your AnswerSign up or log in, post as a guest. Required, but never shown By clicking “Post Your Answer”, you agree to our terms of service and acknowledge you have read our privacy policy . Not the answer you're looking for? Browse other questions tagged hypothesis-testing t-test wilcoxon-mann-whitney-test or ask your own question .
Hot Network Questions
Pardon Our InterruptionAs you were browsing something about your browser made us think you were a bot. There are a few reasons this might happen:
To regain access, please make sure that cookies and JavaScript are enabled before reloading the page.  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
IMAGES
COMMENTS
However, for parametric hypothesis testing, there are additional concerns for ordinal data. Specifically, these variables are less likely to satisfy the analysis' assumptions.
Ordinal is the second of 4 hierarchical levels of measurement: nominal, ordinal, interval, and ratio. The levels of measurement indicate how precisely data is recorded. While nominal and ordinal variables are categorical, interval and ratio variables are quantitative. Nominal data differs from ordinal data because it cannot be ranked in an order.
What does a statistical test do? Statistical tests work by calculating a test statistic - a number that describes how much the relationship between variables in your test differs from the null hypothesis of no relationship. It then calculates a p value (probability value).
Statistical tests for ordinal variables. This tutorial is the third in a series of four. This third part shows you how to apply and interpret the tests for ordinal and interval variables. This link will get you back to the first part of the series. An ordinal variable contains values that can be ordered like ranks and scores.
The tests discussed so far that use the chi-square approximation, including the Pearson and LRT for nominal data as well as the Mantel-Haenszel test for ordinal data, perform well when the contingency tables have a reasonable number of observations in each cell, as already discussed in Lesson 1. When samples are small, the distributions of \ (X ...
Ordinal variables commonly used in clinical and experimental studies with their quantitative alternatives for data collection. N.A. = none available. It is the researcher's decision to present or analyze ordinal variables, whether because there is no quantitative equivalent (for example, cancer staging, satisfaction, relief from symptoms ...
There are 5 main steps in hypothesis testing: State your research hypothesis as a null hypothesis and alternate hypothesis (H o) and (H a or H 1 ). Collect data in a way designed to test the hypothesis. Perform an appropriate statistical test. Decide whether to reject or fail to reject your null hypothesis.
The choice of statistical test used for analysis of data from a research study is crucial in interpreting the results of the study. This article gives an overview of the various factors that determine the selection of a statistical test and lists some ...
Learn about common hypothesis tests for three types of data—continuous, binary, and count data. The data type determines the conclusions that you can draw.
Ordinal data is a type of categorical data in which the values follow a natural order. Ordinal data is the statistical data type that has the following characteristics: Ordinal Data are observed, not measured, are ordered but non-equidistant and have no meaningful zero.
Ranks are themselves ordinal-they tell you information about the order, but no distance between values. Just like other ordinal variables. So while we think of these tests as useful for numerical data that are non-normal or have outliers, they work for ordinal variables as well, especially when there are more than just a few ordered categories.
Ordinal Scale and Hypothesis Testing. Ordinal Scale and Nonparametric Methods. preamble: Ordinal scales involve ranking. The use of numbers in an ordinal scale formation implies greater than or less than relationship. It does not in any way imply as to how much more or how much less. In other words, in any ordinal scale, objects are ranked but ...
Measurement Scales vs. Statistical Tests Parametric tests most appropriate for... Ratio data, interval data Non-parametric tests most appropriate for... Ordinal data, nominal data (although limited use for ratio and interval data)
Ordinal data can also be analyzed using advanced statistical analysis tools such as hypothesis testing. Note that the standard parametric methods such as t-test or ANOVA cannot be applied to such types of data.
1. Suppose I want to compare how different categories of deprivation or education differs between two groups. Deprivation and education are obviously ordinal variables, in this hypothetical example let's say there are 10 levels (deciles) for deprivation, and 5 levels for highest education (primary, secondary, apprenticeship, university, higher ...
Moreover, the measure ϕ gives rise to a general procedure for testing the hypothesis of partial independence. Our framework also permits visualization tools, such as partial regression plots and three-dimensional P-P plots, to examine the association structure, which is otherwise unfeasible for ordinal data.
We propose using the generalized odds ratio (GOR) for paired sample data to measure the relative effect on patient responses for both treatment and period in ordinal data under a simple crossover trial. Assuming the treatment and period effects are multiplicative, we note that one can easily derive the maximum likelihood estimator (LE) in ...
Hypothesis test on ordinal data. In summary: DIn summary, the question is asking how to test whether a population is 95% satisfied. There is no one-size-fits-all answer to this question, as the methods used will depend on the data and the hypothesis being tested.
This "non-parametric T test" is asymptotically equivalent to the Mann-Whitney test. Another approach is to use ordinal logistic regression. This is also called a proportional odds model. Expand the data using a full data matrix of 252+98 observations or use a weighted dataset for the 10 tabular values:
2 point: 1 for each hypothesis. If symbol notation or written format is missing for a hypothesis, deduct .5 2. Conduct a one-tailed hypothesis test, with α = .05. Identify the critical t-value from a t-table (e.g., in the course module entitled "Learning Resources", on the page entitled "Statistical Reference Tables: Z, t, Chi square"). 1 point