Have a language expert improve your writing
Run a free plagiarism check in 10 minutes, generate accurate citations for free.
- Knowledge Base

Hypothesis Testing | A Step-by-Step Guide with Easy Examples
Published on November 8, 2019 by Rebecca Bevans . Revised on June 22, 2023.
Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics . It is most often used by scientists to test specific predictions, called hypotheses, that arise from theories.
There are 5 main steps in hypothesis testing:
- State your research hypothesis as a null hypothesis and alternate hypothesis (H o ) and (H a or H 1 ).
- Collect data in a way designed to test the hypothesis.
- Perform an appropriate statistical test .
- Decide whether to reject or fail to reject your null hypothesis.
- Present the findings in your results and discussion section.
Though the specific details might vary, the procedure you will use when testing a hypothesis will always follow some version of these steps.
Table of contents
Step 1: state your null and alternate hypothesis, step 2: collect data, step 3: perform a statistical test, step 4: decide whether to reject or fail to reject your null hypothesis, step 5: present your findings, other interesting articles, frequently asked questions about hypothesis testing.
After developing your initial research hypothesis (the prediction that you want to investigate), it is important to restate it as a null (H o ) and alternate (H a ) hypothesis so that you can test it mathematically.
The alternate hypothesis is usually your initial hypothesis that predicts a relationship between variables. The null hypothesis is a prediction of no relationship between the variables you are interested in.
- H 0 : Men are, on average, not taller than women. H a : Men are, on average, taller than women.
Here's why students love Scribbr's proofreading services
Discover proofreading & editing
For a statistical test to be valid , it is important to perform sampling and collect data in a way that is designed to test your hypothesis. If your data are not representative, then you cannot make statistical inferences about the population you are interested in.
There are a variety of statistical tests available, but they are all based on the comparison of within-group variance (how spread out the data is within a category) versus between-group variance (how different the categories are from one another).
If the between-group variance is large enough that there is little or no overlap between groups, then your statistical test will reflect that by showing a low p -value . This means it is unlikely that the differences between these groups came about by chance.
Alternatively, if there is high within-group variance and low between-group variance, then your statistical test will reflect that with a high p -value. This means it is likely that any difference you measure between groups is due to chance.
Your choice of statistical test will be based on the type of variables and the level of measurement of your collected data .
- an estimate of the difference in average height between the two groups.
- a p -value showing how likely you are to see this difference if the null hypothesis of no difference is true.
Based on the outcome of your statistical test, you will have to decide whether to reject or fail to reject your null hypothesis.
In most cases you will use the p -value generated by your statistical test to guide your decision. And in most cases, your predetermined level of significance for rejecting the null hypothesis will be 0.05 – that is, when there is a less than 5% chance that you would see these results if the null hypothesis were true.
In some cases, researchers choose a more conservative level of significance, such as 0.01 (1%). This minimizes the risk of incorrectly rejecting the null hypothesis ( Type I error ).
The results of hypothesis testing will be presented in the results and discussion sections of your research paper , dissertation or thesis .
In the results section you should give a brief summary of the data and a summary of the results of your statistical test (for example, the estimated difference between group means and associated p -value). In the discussion , you can discuss whether your initial hypothesis was supported by your results or not.
In the formal language of hypothesis testing, we talk about rejecting or failing to reject the null hypothesis. You will probably be asked to do this in your statistics assignments.
However, when presenting research results in academic papers we rarely talk this way. Instead, we go back to our alternate hypothesis (in this case, the hypothesis that men are on average taller than women) and state whether the result of our test did or did not support the alternate hypothesis.
If your null hypothesis was rejected, this result is interpreted as “supported the alternate hypothesis.”
These are superficial differences; you can see that they mean the same thing.
You might notice that we don’t say that we reject or fail to reject the alternate hypothesis . This is because hypothesis testing is not designed to prove or disprove anything. It is only designed to test whether a pattern we measure could have arisen spuriously, or by chance.
If we reject the null hypothesis based on our research (i.e., we find that it is unlikely that the pattern arose by chance), then we can say our test lends support to our hypothesis . But if the pattern does not pass our decision rule, meaning that it could have arisen by chance, then we say the test is inconsistent with our hypothesis .
If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.
- Normal distribution
- Descriptive statistics
- Measures of central tendency
- Correlation coefficient
Methodology
- Cluster sampling
- Stratified sampling
- Types of interviews
- Cohort study
- Thematic analysis
Research bias
- Implicit bias
- Cognitive bias
- Survivorship bias
- Availability heuristic
- Nonresponse bias
- Regression to the mean
Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.
A hypothesis states your predictions about what your research will find. It is a tentative answer to your research question that has not yet been tested. For some research projects, you might have to write several hypotheses that address different aspects of your research question.
A hypothesis is not just a guess — it should be based on existing theories and knowledge. It also has to be testable, which means you can support or refute it through scientific research methods (such as experiments, observations and statistical analysis of data).
Null and alternative hypotheses are used in statistical hypothesis testing . The null hypothesis of a test always predicts no effect or no relationship between variables, while the alternative hypothesis states your research prediction of an effect or relationship.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
Bevans, R. (2023, June 22). Hypothesis Testing | A Step-by-Step Guide with Easy Examples. Scribbr. Retrieved September 3, 2024, from https://www.scribbr.com/statistics/hypothesis-testing/
Is this article helpful?
Rebecca Bevans
Other students also liked, choosing the right statistical test | types & examples, understanding p values | definition and examples, what is your plagiarism score.
Reset password New user? Sign up
Existing user? Log in
Hypothesis Testing
Already have an account? Log in here.
A hypothesis test is a statistical inference method used to test the significance of a proposed (hypothesized) relation between population statistics (parameters) and their corresponding sample estimators . In other words, hypothesis tests are used to determine if there is enough evidence in a sample to prove a hypothesis true for the entire population.
The test considers two hypotheses: the null hypothesis , which is a statement meant to be tested, usually something like "there is no effect" with the intention of proving this false, and the alternate hypothesis , which is the statement meant to stand after the test is performed. The two hypotheses must be mutually exclusive ; moreover, in most applications, the two are complementary (one being the negation of the other). The test works by comparing the \(p\)-value to the level of significance (a chosen target). If the \(p\)-value is less than or equal to the level of significance, then the null hypothesis is rejected.
When analyzing data, only samples of a certain size might be manageable as efficient computations. In some situations the error terms follow a continuous or infinite distribution, hence the use of samples to suggest accuracy of the chosen test statistics. The method of hypothesis testing gives an advantage over guessing what distribution or which parameters the data follows.
Definitions and Methodology
Hypothesis test and confidence intervals.
In statistical inference, properties (parameters) of a population are analyzed by sampling data sets. Given assumptions on the distribution, i.e. a statistical model of the data, certain hypotheses can be deduced from the known behavior of the model. These hypotheses must be tested against sampled data from the population.
The null hypothesis \((\)denoted \(H_0)\) is a statement that is assumed to be true. If the null hypothesis is rejected, then there is enough evidence (statistical significance) to accept the alternate hypothesis \((\)denoted \(H_1).\) Before doing any test for significance, both hypotheses must be clearly stated and non-conflictive, i.e. mutually exclusive, statements. Rejecting the null hypothesis, given that it is true, is called a type I error and it is denoted \(\alpha\), which is also its probability of occurrence. Failing to reject the null hypothesis, given that it is false, is called a type II error and it is denoted \(\beta\), which is also its probability of occurrence. Also, \(\alpha\) is known as the significance level , and \(1-\beta\) is known as the power of the test. \(H_0\) \(\textbf{is true}\)\(\hspace{15mm}\) \(H_0\) \(\textbf{is false}\) \(\textbf{Reject}\) \(H_0\)\(\hspace{10mm}\) Type I error Correct Decision \(\textbf{Reject}\) \(H_1\) Correct Decision Type II error The test statistic is the standardized value following the sampled data under the assumption that the null hypothesis is true, and a chosen particular test. These tests depend on the statistic to be studied and the assumed distribution it follows, e.g. the population mean following a normal distribution. The \(p\)-value is the probability of observing an extreme test statistic in the direction of the alternate hypothesis, given that the null hypothesis is true. The critical value is the value of the assumed distribution of the test statistic such that the probability of making a type I error is small.
Methodologies: Given an estimator \(\hat \theta\) of a population statistic \(\theta\), following a probability distribution \(P(T)\), computed from a sample \(\mathcal{S},\) and given a significance level \(\alpha\) and test statistic \(t^*,\) define \(H_0\) and \(H_1;\) compute the test statistic \(t^*.\) \(p\)-value Approach (most prevalent): Find the \(p\)-value using \(t^*\) (right-tailed). If the \(p\)-value is at most \(\alpha,\) reject \(H_0\). Otherwise, reject \(H_1\). Critical Value Approach: Find the critical value solving the equation \(P(T\geq t_\alpha)=\alpha\) (right-tailed). If \(t^*>t_\alpha\), reject \(H_0\). Otherwise, reject \(H_1\). Note: Failing to reject \(H_0\) only means inability to accept \(H_1\), and it does not mean to accept \(H_0\).
Assume a normally distributed population has recorded cholesterol levels with various statistics computed. From a sample of 100 subjects in the population, the sample mean was 214.12 mg/dL (milligrams per deciliter), with a sample standard deviation of 45.71 mg/dL. Perform a hypothesis test, with significance level 0.05, to test if there is enough evidence to conclude that the population mean is larger than 200 mg/dL. Hypothesis Test We will perform a hypothesis test using the \(p\)-value approach with significance level \(\alpha=0.05:\) Define \(H_0\): \(\mu=200\). Define \(H_1\): \(\mu>200\). Since our values are normally distributed, the test statistic is \(z^*=\frac{\bar X - \mu_0}{\frac{s}{\sqrt{n}}}=\frac{214.12 - 200}{\frac{45.71}{\sqrt{100}}}\approx 3.09\). Using a standard normal distribution, we find that our \(p\)-value is approximately \(0.001\). Since the \(p\)-value is at most \(\alpha=0.05,\) we reject \(H_0\). Therefore, we can conclude that the test shows sufficient evidence to support the claim that \(\mu\) is larger than \(200\) mg/dL.
If the sample size was smaller, the normal and \(t\)-distributions behave differently. Also, the question itself must be managed by a double-tail test instead.
Assume a population's cholesterol levels are recorded and various statistics are computed. From a sample of 25 subjects, the sample mean was 214.12 mg/dL (milligrams per deciliter), with a sample standard deviation of 45.71 mg/dL. Perform a hypothesis test, with significance level 0.05, to test if there is enough evidence to conclude that the population mean is not equal to 200 mg/dL. Hypothesis Test We will perform a hypothesis test using the \(p\)-value approach with significance level \(\alpha=0.05\) and the \(t\)-distribution with 24 degrees of freedom: Define \(H_0\): \(\mu=200\). Define \(H_1\): \(\mu\neq 200\). Using the \(t\)-distribution, the test statistic is \(t^*=\frac{\bar X - \mu_0}{\frac{s}{\sqrt{n}}}=\frac{214.12 - 200}{\frac{45.71}{\sqrt{25}}}\approx 1.54\). Using a \(t\)-distribution with 24 degrees of freedom, we find that our \(p\)-value is approximately \(2(0.068)=0.136\). We have multiplied by two since this is a two-tailed argument, i.e. the mean can be smaller than or larger than. Since the \(p\)-value is larger than \(\alpha=0.05,\) we fail to reject \(H_0\). Therefore, the test does not show sufficient evidence to support the claim that \(\mu\) is not equal to \(200\) mg/dL.
The complement of the rejection on a two-tailed hypothesis test (with significance level \(\alpha\)) for a population parameter \(\theta\) is equivalent to finding a confidence interval \((\)with confidence level \(1-\alpha)\) for the population parameter \(\theta\). If the assumption on the parameter \(\theta\) falls inside the confidence interval, then the test has failed to reject the null hypothesis \((\)with \(p\)-value greater than \(\alpha).\) Otherwise, if \(\theta\) does not fall in the confidence interval, then the null hypothesis is rejected in favor of the alternate \((\)with \(p\)-value at most \(\alpha).\)
- Statistics (Estimation)
- Normal Distribution
- Correlation
- Confidence Intervals
Problem Loading...
Note Loading...
Set Loading...

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
9. Hypothesis Testing
9.1 Hypothesis Testing Problem Solving Steps
- Interpretation : Summarize results in a sentence and/or present a graphic or table.
A generic test statistic may be defined by :
Introduction to Applied Statistics for Psychology Students Copyright © 2022 by Gordon E. Sarty is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.
Share This Book
9.4 Full Hypothesis Test Examples
Tests on means, example 9.8.
Jeffrey, as an eight-year old, established a mean time of 16.43 seconds for swimming the 25-yard freestyle, with a standard deviation of 0.8 seconds . His dad, Frank, thought that Jeffrey could swim the 25-yard freestyle faster using goggles. Frank bought Jeffrey a new pair of expensive goggles and timed Jeffrey for 15 25-yard freestyle swims . For the 15 swims, Jeffrey's mean time was 16 seconds. Frank thought that the goggles helped Jeffrey to swim faster than the 16.43 seconds. Conduct a hypothesis test using a preset α = 0.05.
Set up the Hypothesis Test:
Since the problem is about a mean, this is a test of a single population mean .
Set the null and alternative hypothesis:
In this case there is an implied challenge or claim. This is that the goggles will reduce the swimming time. The effect of this is to set the hypothesis as a one-tailed test. The claim will always be in the alternative hypothesis because the burden of proof always lies with the alternative. Remember that the status quo must be defeated with a high degree of confidence, in this case 95 % confidence. The null and alternative hypotheses are thus:
H 0 : μ ≥ 16.43 H a : μ < 16.43
For Jeffrey to swim faster, his time will be less than 16.43 seconds. The "<" tells you this is left-tailed.
Determine the distribution needed:
Random variable: X ¯ X ¯ = the mean time to swim the 25-yard freestyle.
Distribution for the test statistic:
The sample size is less than 30 and we do not know the population standard deviation so this is a t-test. and the proper formula is: t c = X ¯ - μ 0 σ / n t c = X ¯ - μ 0 σ / n
μ 0 = 16.43 comes from H 0 and not the data. X ¯ X ¯ = 16. s = 0.8, and n = 15.
Our step 2, setting the level of significance, has already been determined by the problem, .05 for a 95 % significance level. It is worth thinking about the meaning of this choice. The Type I error is to conclude that Jeffrey swims the 25-yard freestyle, on average, in less than 16.43 seconds when, in fact, he actually swims the 25-yard freestyle, on average, in 16.43 seconds. (Reject the null hypothesis when the null hypothesis is true.) For this case the only concern with a Type I error would seem to be that Jeffery’s dad may fail to bet on his son’s victory because he does not have appropriate confidence in the effect of the goggles.
To find the critical value we need to select the appropriate test statistic. We have concluded that this is a t-test on the basis of the sample size and that we are interested in a population mean. We can now draw the graph of the t-distribution and mark the critical value. For this problem the degrees of freedom are n-1, or 14. Looking up 14 degrees of freedom at the 0.05 column of the t-table we find 1.761. This is the critical value and we can put this on our graph.
Step 3 is the calculation of the test statistic using the formula we have selected. We find that the calculated test statistic is 2.08, meaning that the sample mean is 2.08 standard deviations away from the hypothesized mean of 16.43.
Step 4 has us compare the test statistic and the critical value and mark these on the graph. We see that the test statistic is in the tail and thus we move to step 4 and reach a conclusion. The probability that an average time of 16 minutes could come from a distribution with a population mean of 16.43 minutes is too unlikely for us to accept the null hypothesis. We cannot accept the null.
Step 5 has us state our conclusions first formally and then less formally. A formal conclusion would be stated as: “With a 95% level of significance we cannot accept the null hypothesis that the swimming time with goggles comes from a distribution with a population mean time of 16.43 minutes.” Less formally, “With 95% significance we believe that the goggles improves swimming speed”
If we wished to use the p-value system of reaching a conclusion we would calculate the statistic and take the additional step to find the probability of being 2.08 standard deviations from the mean on a t-distribution. This value is .0187. Comparing this to the α-level of .05 we see that we cannot accept the null. The p-value has been put on the graph as the shaded area beyond -2.08 and it shows that it is smaller than the hatched area which is the alpha level of 0.05. Both methods reach the same conclusion that we cannot accept the null hypothesis.
The mean throwing distance of a football for Marco, a high school freshman quarterback, is 40 yards, with a standard deviation of two yards. The team coach tells Marco to adjust his grip to get more distance. The coach records the distances for 20 throws. For the 20 throws, Marco’s mean distance was 45 yards. The coach thought the different grip helped Marco throw farther than 40 yards. Conduct a hypothesis test using a preset α = 0.05. Assume the throw distances for footballs are normal.
First, determine what type of test this is, set up the hypothesis test, find the p -value, sketch the graph, and state your conclusion.
Example 9.9
Jane has just begun her new job as on the sales force of a very competitive company. In a sample of 16 sales calls it was found that she closed the contract for an average value of 108 dollars with a standard deviation of 12 dollars. Test at 5% significance that the population mean is at least 100 dollars against the alternative that it is less than 100 dollars. Company policy requires that new members of the sales force must exceed an average of $100 per contract during the trial employment period. Can we conclude that Jane has met this requirement at the significance level of 95%?
- H 0 : µ ≤ 100 H a : µ > 100 The null and alternative hypothesis are for the parameter µ because the number of dollars of the contracts is a continuous random variable. Also, this is a one-tailed test because the company has only an interested if the number of dollars per contact is below a particular number not "too high" a number. This can be thought of as making a claim that the requirement is being met and thus the claim is in the alternative hypothesis.
- Test statistic: t c = x ¯ − µ 0 s n = 108 − 100 ( 12 16 ) = 2.67 t c = x ¯ − µ 0 s n = 108 − 100 ( 12 16 ) = 2.67
- Critical value: t a = 1.753 t a = 1.753 with n-1 degrees of freedom= 15
The test statistic is a Student's t because the sample size is below 30; therefore, we cannot use the normal distribution. Comparing the calculated value of the test statistic and the critical value of t t ( t a ) ( t a ) at a 5% significance level, we see that the calculated value is in the tail of the distribution. Thus, we conclude that 108 dollars per contract is significantly larger than the hypothesized value of 100 and thus we cannot accept the null hypothesis. There is evidence that supports Jane's performance meets company standards.
It is believed that a stock price for a particular company will grow at a rate of $5 per week with a standard deviation of $1. An investor believes the stock won’t grow as quickly. The changes in stock price is recorded for ten weeks and are as follows: $4, $3, $2, $3, $1, $7, $2, $1, $1, $2. Perform a hypothesis test using a 5% level of significance. State the null and alternative hypotheses, state your conclusion, and identify the Type I errors.
Example 9.10
A manufacturer of salad dressings uses machines to dispense liquid ingredients into bottles that move along a filling line. The machine that dispenses salad dressings is working properly when 8 ounces are dispensed. Suppose that the average amount dispensed in a particular sample of 35 bottles is 7.91 ounces with a variance of 0.03 ounces squared, s 2 s 2 . Is there evidence that the machine should be stopped and production wait for repairs? The lost production from a shutdown is potentially so great that management feels that the level of significance in the analysis should be 99%.
Again we will follow the steps in our analysis of this problem.
STEP 1 : Set the Null and Alternative Hypothesis. The random variable is the quantity of fluid placed in the bottles. This is a continuous random variable and the parameter we are interested in is the mean. Our hypothesis therefore is about the mean. In this case we are concerned that the machine is not filling properly. From what we are told it does not matter if the machine is over-filling or under-filling, both seem to be an equally bad error. This tells us that this is a two-tailed test: if the machine is malfunctioning it will be shutdown regardless if it is from over-filling or under-filling. The null and alternative hypotheses are thus:
STEP 2 : Decide the level of significance and draw the graph showing the critical value.
This problem has already set the level of significance at 99%. The decision seems an appropriate one and shows the thought process when setting the significance level. Management wants to be very certain, as certain as probability will allow, that they are not shutting down a machine that is not in need of repair. To draw the distribution and the critical value, we need to know which distribution to use. Because this is a continuous random variable and we are interested in the mean, and the sample size is greater than 30, the appropriate distribution is the normal distribution and the relevant critical value is 2.575 from the normal table or the t-table at 0.005 column and infinite degrees of freedom. We draw the graph and mark these points.
STEP 3 : Calculate sample parameters and the test statistic. The sample parameters are provided, the sample mean is 7.91 and the sample variance is .03 and the sample size is 35. We need to note that the sample variance was provided not the sample standard deviation, which is what we need for the formula. Remembering that the standard deviation is simply the square root of the variance, we therefore know the sample standard deviation, s, is 0.173. With this information we calculate the test statistic as -3.07, and mark it on the graph.
STEP 4 : Compare test statistic and the critical values Now we compare the test statistic and the critical value by placing the test statistic on the graph. We see that the test statistic is in the tail, decidedly greater than the critical value of 2.575. We note that even the very small difference between the hypothesized value and the sample value is still a large number of standard deviations. The sample mean is only 0.08 ounces different from the required level of 8 ounces, but it is 3 plus standard deviations away and thus we cannot accept the null hypothesis.
STEP 5 : Reach a Conclusion
Three standard deviations of a test statistic will guarantee that the test will fail. The probability that anything is within three standard deviations is almost zero. Actually it is 0.0026 on the normal distribution, which is certainly almost zero in a practical sense. Our formal conclusion would be “ At a 99% level of significance we cannot accept the hypothesis that the sample mean came from a distribution with a mean of 8 ounces” Or less formally, and getting to the point, “At a 99% level of significance we conclude that the machine is under filling the bottles and is in need of repair”.
Hypothesis Test for Proportions
Just as there were confidence intervals for proportions, or more formally, the population parameter p of the binomial distribution, there is the ability to test hypotheses concerning p .
The population parameter for the binomial is p . The estimated value (point estimate) for p is p′ where p′ = x/n , x is the number of successes in the sample and n is the sample size.
When you perform a hypothesis test of a population proportion p , you take a simple random sample from the population. The conditions for a binomial distribution must be met, which are: there are a certain number n of independent trials meaning random sampling, the outcomes of any trial are binary, success or failure, and each trial has the same probability of a success p . The shape of the binomial distribution needs to be similar to the shape of the normal distribution. To ensure this, the quantities np′ and nq′ must both be greater than five ( np′ > 5 and nq′ > 5). In this case the binomial distribution of a sample (estimated) proportion can be approximated by the normal distribution with μ = np μ = np and σ = npq σ = npq . Remember that q = 1 – p q = 1 – p . There is no distribution that can correct for this small sample bias and thus if these conditions are not met we simply cannot test the hypothesis with the data available at that time. We met this condition when we first were estimating confidence intervals for p .
Again, we begin with the standardizing formula modified because this is the distribution of a binomial.
Substituting p 0 p 0 , the hypothesized value of p , we have:
This is the test statistic for testing hypothesized values of p , where the null and alternative hypotheses take one of the following forms:
| Two-tailed test | One-tailed test | One-tailed test |
|---|---|---|
| H : p = p | H : p ≤ p | H : p ≥ p |
| H : p ≠ p | H : p > p | H : p < p |
The decision rule stated above applies here also: if the calculated value of Z c shows that the sample proportion is "too many" standard deviations from the hypothesized proportion, the null hypothesis cannot be accepted. The decision as to what is "too many" is pre-determined by the analyst depending on the level of significance required in the test.
Example 9.11
The mortgage department of a large bank is interested in the nature of loans of first-time borrowers. This information will be used to tailor their marketing strategy. They believe that 50% of first-time borrowers take out smaller loans than other borrowers. They perform a hypothesis test to determine if the percentage is the same or different from 50% . They sample 100 first-time borrowers and find 53 of these loans are smaller that the other borrowers. For the hypothesis test, they choose a 5% level of significance.
STEP 1 : Set the null and alternative hypothesis.
H 0 : p = 0.50 H a : p ≠ 0.50
The words "is the same or different from" tell you this is a two-tailed test. The Type I and Type II errors are as follows: The Type I error is to conclude that the proportion of borrowers is different from 50% when, in fact, the proportion is actually 50%. (Reject the null hypothesis when the null hypothesis is true). The Type II error is there is not enough evidence to conclude that the proportion of first time borrowers differs from 50% when, in fact, the proportion does differ from 50%. (You fail to reject the null hypothesis when the null hypothesis is false.)
STEP 2 : Decide the level of significance and draw the graph showing the critical value
The level of significance has been set by the problem at the 95% level. Because this is two-tailed test one-half of the alpha value will be in the upper tail and one-half in the lower tail as shown on the graph. The critical value for the normal distribution at the 95% level of confidence is 1.96. This can easily be found on the student’s t-table at the very bottom at infinite degrees of freedom remembering that at infinity the t-distribution is the normal distribution. Of course the value can also be found on the normal table but you have go looking for one-half of 95 (0.475) inside the body of the table and then read out to the sides and top for the number of standard deviations.
STEP 3 : Calculate the sample parameters and critical value of the test statistic.
The test statistic is a normal distribution, Z, for testing proportions and is:
For this case, the sample of 100 found 53 first-time borrowers were different from other borrowers. The sample proportion, p′ = 53/100= 0.53 The test question, therefore, is : “Is 0.53 significantly different from .50?” Putting these values into the formula for the test statistic we find that 0.53 is only 0.60 standard deviations away from .50. This is barely off of the mean of the standard normal distribution of zero. There is virtually no difference from the sample proportion and the hypothesized proportion in terms of standard deviations.
STEP 4 : Compare the test statistic and the critical value.
The calculated value is well within the critical values of ± 1.96 standard deviations and thus we cannot reject the null hypothesis. To reject the null hypothesis we need significant evident of difference between the hypothesized value and the sample value. In this case the sample value is very nearly the same as the hypothesized value measured in terms of standard deviations.
STEP 5 : Reach a conclusion
The formal conclusion would be “At a 95% level of significance we cannot reject the null hypothesis that 50% of first-time borrowers have the same size loans as other borrowers”. Less formally we would say that “There is no evidence that one-half of first-time borrowers are significantly different in loan size from other borrowers”. Notice the length to which the conclusion goes to include all of the conditions that are attached to the conclusion. Statisticians for all the criticism they receive, are careful to be very specific even when this seems trivial. Statisticians cannot say more than they know and the data constrain the conclusion to be within the metes and bounds of the data.
Try It 9.11
A teacher believes that 85% of students in the class will want to go on a field trip to the local zoo. She performs a hypothesis test to determine if the percentage is the same or different from 85%. The teacher samples 50 students and 39 reply that they would want to go to the zoo. For the hypothesis test, use a 1% level of significance.

Example 9.12
Suppose a consumer group suspects that the proportion of households that have three or more cell phones is 30%. A cell phone company has reason to believe that the proportion is not 30%. Before they start a big advertising campaign, they conduct a hypothesis test. Their marketing people survey 150 households with the result that 43 of the households have three or more cell phones.
Here is an abbreviate version of the system to solve hypothesis tests applied to a test on a proportions.
Example 9.13
The National Institute of Standards and Technology provides exact data on conductivity properties of materials. Following are conductivity measurements for 11 randomly selected pieces of a particular type of glass.
1.11; 1.07; 1.11; 1.07; 1.12; 1.08; .98; .98 1.02; .95; .95 Is there convincing evidence that the average conductivity of this type of glass is greater than one? Use a significance level of 0.05.
Let’s follow a four-step process to answer this statistical question.
- H 0 : μ ≤ 1
- H a : μ > 1
- Plan : We are testing a sample mean without a known population standard deviation with less than 30 observations. Therefore, we need to use a Student's-t distribution. Assume the underlying population is normal.
- Do the calculations and draw the graph .
- State the Conclusions : We cannot accept the null hypothesis. It is reasonable to state that the data supports the claim that the average conductivity level is greater than one.
Example 9.14
In a study of 420,019 cell phone users, 172 of the subjects developed brain cancer. Test the claim that cell phone users developed brain cancer at a greater rate than that for non-cell phone users (the rate of brain cancer for non-cell phone users is 0.0340%). Since this is a critical issue, use a 0.005 significance level. Explain why the significance level should be so low in terms of a Type I error.
- H 0 : p ≤ 0.00034
- H a : p > 0.00034
If we commit a Type I error, we are essentially accepting a false claim. Since the claim describes cancer-causing environments, we want to minimize the chances of incorrectly identifying causes of cancer.
- We will be testing a sample proportion with x = 172 and n = 420,019. The sample is sufficiently large because we have np' = 420,019(0.00034) = 142.8, nq' = 420,019(0.99966) = 419,876.2, two independent outcomes, and a fixed probability of success p' = 0.00034. Thus we will be able to generalize our results to the population.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/introductory-business-statistics/pages/1-introduction
- Authors: Alexander Holmes, Barbara Illowsky, Susan Dean
- Publisher/website: OpenStax
- Book title: Introductory Business Statistics
- Publication date: Nov 29, 2017
- Location: Houston, Texas
- Book URL: https://openstax.org/books/introductory-business-statistics/pages/1-introduction
- Section URL: https://openstax.org/books/introductory-business-statistics/pages/9-4-full-hypothesis-test-examples
© Jun 23, 2022 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
5.5 Introduction to Hypothesis Tests

One job of a statistician is to make statistical inferences about populations based on samples taken from the population. Confidence intervals are one way to estimate a population parameter.
Another way to make a statistical inference is to make a decision about a parameter. For instance, a car dealership advertises that its new small truck gets 35 miles per gallon on average. A tutoring service claims that its method of tutoring helps 90% of its students get an A or a B. A company says that female managers in their company earn an average of $60,000 per year. A statistician may want to make a decision about or evaluate these claims. A hypothesis test can be used to do this.
A hypothesis test involves collecting data from a sample and evaluating the data. Then the statistician makes a decision as to whether or not there is sufficient evidence to reject the null hypothesis based upon analyses of the data.
In this section, you will conduct hypothesis tests on single means when the population standard deviation is known.
Hypothesis testing consists of two contradictory hypotheses or statements, a decision based on the data, and a conclusion. To perform a hypothesis test, a statistician will perform some variation of these steps:
- Define hypotheses.
- Collect and/or use the sample data to determine the correct distribution to use.
- Calculate test statistic.
- Make a decision.
- Write a conclusion.
Defining your hypotheses
The actual test begins by considering two hypotheses: the null hypothesis and the alternative hypothesis. These hypotheses contain opposing viewpoints.
The null hypothesis ( H 0 ) is often a statement of the accepted historical value or norm. This is your starting point that you must assume from the beginning in order to show an effect exists.
The alternative hypothesis ( H a ) is a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .
Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.
After you have determined which hypothesis the sample supports, you make a decision . There are two options for a decision. They are “reject H 0 ” if the sample information favors the alternative hypothesis or “do not reject H 0 ” or “decline to reject H 0 ” if the sample information is insufficient to reject the null hypothesis.
The following table shows mathematical symbols used in H 0 and H a :
| equal (=) | not equal (≠) greater than (>) less than (<) |
| equal (=) | less than (<) |
| equal (=) | more than (>) |
NOTE: H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol in the alternative hypothesis depends on the wording of the hypothesis test. Despite this, many researchers may use =, ≤, or ≥ in the null hypothesis. This practice is acceptable because our only decision is to reject or not reject the null hypothesis.
We want to test whether the mean GPA of students in American colleges is 2.0 (out of 4.0). The null hypothesis is: H 0 : μ = 2.0. What is the alternative hypothesis?
A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.
Using the Sample to Test the Null Hypothesis
Once you have defined your hypotheses, the next step in the process is to collect sample data. In a classroom context, the data or summary statistics will usually be given to you.
Then you will have to determine the correct distribution to perform the hypothesis test, given the assumptions you are able to make about the situation. Right now, we are demonstrating these ideas in a test for a mean when the population standard deviation is known using the z distribution. We will see other scenarios in the future.
Calculating a Test Statistic
Next you will start evaluating the data. This begins with calculating your test statistic , which is a measure of the distance between what you observed and what you are assuming to be true. In this context, your test statistic, z ο , quantifies the number of standard deviations between the sample mean, x, and the population mean, µ . Calculating the test statistic is analogous to the previously discussed process of standardizing observations with z -scores:
where µ o is the value assumed to be true in the null hypothesis.
Making a Decision
Once you have your test statistic, there are two methods to use it to make your decision:
- Critical value method (discussed further in later chapters)
- p -value method (our current focus)
p -Value Method
To find a p -value , we use the test statistic to calculate the actual probability of getting the test result. Formally, the p -value is the probability that, if the null hypothesis is true, the results from another randomly selected sample will be as extreme or more extreme as the results obtained from the given sample.
A large p -value calculated from the data indicates that we should not reject the null hypothesis. The smaller the p -value, the more unlikely the outcome and the stronger the evidence is against the null hypothesis. We would reject the null hypothesis if the evidence is strongly against it.
Draw a graph that shows the p -value. The hypothesis test is easier to perform if you use a graph because you see the problem more clearly.
Suppose a baker claims that his bread height is more than 15 cm on average. Several of his customers do not believe him. To persuade his customers that he is right, the baker decides to do a hypothesis test. He bakes ten loaves of bread. The mean height of the sample loaves is 17 cm. The baker knows from baking hundreds of loaves of bread that the standard deviation for the height is 0.5 cm and the distribution of heights is normal.
The null hypothesis could be H 0 : μ ≤ 15.
The alternate hypothesis is H a : μ > 15.
The words “is more than” calls for the use of the > symbol, so “ μ > 15″ goes into the alternate hypothesis. The null hypothesis must contradict the alternate hypothesis.
Suppose the null hypothesis is true (the mean height of the loaves is no more than 15 cm). Then, is the mean height (17 cm) calculated from the sample unexpectedly large? The hypothesis test works by asking how unlikely the sample mean would be if the null hypothesis were true. The graph shows how far out the sample mean is on the normal curve. The p -value is the probability that, if we were to take other samples, any other sample mean would fall at least as far out as 17 cm.
This means that the p -value is the probability that a sample mean is the same or greater than 17 cm when the population mean is, in fact, 15 cm. We can calculate this probability using the normal distribution for means.
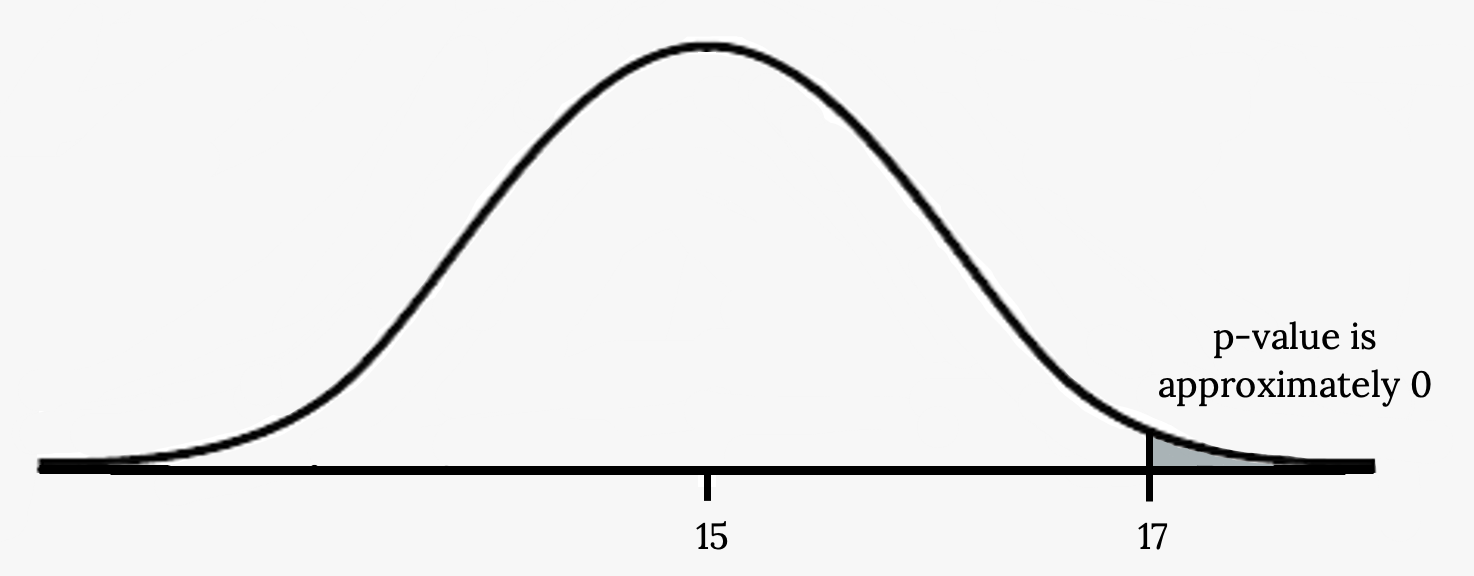
A p -value of approximately zero tells us that it is highly unlikely that a loaf of bread rises no more than 15 cm on average. That is, almost 0% of all loaves of bread would be at least as high as 17 cm purely by CHANCE had the population mean height really been 15 cm. Because the outcome of 17 cm is so unlikely (meaning it is happening NOT by chance alone), we conclude that the evidence is strongly against the null hypothesis that the mean height would be at most 15 cm. There is sufficient evidence that the true mean height for the population of the baker’s loaves of bread is greater than 15 cm.
A normal distribution has a standard deviation of one. We want to verify a claim that the mean is greater than 12. A sample of 36 is taken with a sample mean of 12.5.
Find the p -value.
Decision and Conclusion
A systematic way to decide whether to reject or not reject the null hypothesis is to compare the p -value and a preset or preconceived α (also called a significance level ). A preset α is the probability of a type I error (rejecting the null hypothesis when the null hypothesis is true). It may or may not be given to you at the beginning of the problem. If there is no given preconceived α , then use α = 0.05.
When you make a decision to reject or not reject H 0 , do as follows:
- If α > p -value, reject H 0 . The results of the sample data are statistically significant . You can say there is sufficient evidence to conclude that H 0 is an incorrect belief and that the alternative hypothesis, H a , may be correct.
- If α ≤ p -value, fail to reject H 0 . The results of the sample data are not significant. There is not sufficient evidence to conclude that the alternative hypothesis, H a , may be correct.
After you make your decision, write a thoughtful conclusion in the context of the scenario incorporating the hypotheses.
NOTE: When you “do not reject H 0 ,” it does not mean that you should believe that H 0 is true. It simply means that the sample data have failed to provide sufficient evidence to cast serious doubt about the truthfulness of H o .
When using the p -value to evaluate a hypothesis test, the following rhymes can come in handy:
If the p -value is low, the null must go.
If the p -value is high, the null must fly.
This memory aid relates a p -value less than the established alpha (“the p -value is low”) as rejecting the null hypothesis and, likewise, relates a p -value higher than the established alpha (“the p -value is high”) as not rejecting the null hypothesis.
Fill in the blanks:
- Reject the null hypothesis when .
- The results of the sample data .
- Do not reject the null when hypothesis when .
It’s a Boy Genetics Labs claim their procedures improve the chances of a boy being born. The results for a test of a single population proportion are as follows:
- H 0 : p = 0.50, H a : p > 0.50
- p -value = 0.025
Interpret the results and state a conclusion in simple, non-technical terms.
Click here for more multimedia resources, including podcasts, videos, lecture notes, and worked examples.
Figure References
Figure 5.11: Alora Griffiths (2019). dalmatian puppy near man in blue shorts kneeling. Unsplash license. https://unsplash.com/photos/7aRQZtLsvqw
Figure 5.13: Kindred Grey (2020). Bread height probability. CC BY-SA 4.0.
A decision-making procedure for determining whether sample evidence supports a hypothesis
The claim that is assumed to be true and is tested in a hypothesis test
A working hypothesis that is contradictory to the null hypothesis
A measure of the difference between observations and the hypothesized (or claimed) value
The probability that an event will occur, assuming the null hypothesis is true
Probability that a true null hypothesis will be rejected, also known as type I error and denoted by α
Finding sufficient evidence that the observed effect is not just due to variability, often from rejecting the null hypothesis
Significant Statistics Copyright © 2024 by John Morgan Russell, OpenStaxCollege, OpenIntro is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License , except where otherwise noted.
Share This Book
User Preferences
Content preview.
Arcu felis bibendum ut tristique et egestas quis:
- Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
- Duis aute irure dolor in reprehenderit in voluptate
- Excepteur sint occaecat cupidatat non proident
Keyboard Shortcuts
11.2.1 - five step hypothesis testing procedure.
The examples on the following pages use the five step hypothesis testing procedure outlined below. This is the same procedure that we used to conduct a hypothesis test for a single mean, single proportion, difference in two means, and difference in two proportions.
When conducting a chi-square goodness-of-fit test, it makes the most sense to write the hypotheses first. The hypotheses will depend on the research question. The null hypothesis will always contain the equalities and the alternative hypothesis will be that at least one population proportion is not as specified in the null.
In order to use the chi-square distribution to approximate the sampling distribution, all expected counts must be at least five.
Expected Count
Where \(n\) is the total sample size and \(p_i\) is the hypothesized population proportion in the "ith" group.
To check this assumption, compute all expected counts and confirm that each is at least five.
In Step 1 you already computed the expected counts. Use this formula to compute the chi-square test statistic:
Chi-Square Test Statistic
\(\chi^2=\sum \dfrac{(O-E)^2}{E}\)
Where \(O\) is the observed count for each cell and \(E\) is the expected count for each cell.
Construct a chi-square distribution with degrees of freedom equal to the number of groups minus one. The p-value is the area under that distribution to the right of the test statistic that was computed in Step 2. You can find this area by constructing a probability distribution plot in Minitab.
Unless otherwise stated, use the standard 0.05 alpha level.
\(p \leq \alpha\) reject the null hypothesis.
\(p > \alpha\) fail to reject the null hypothesis.
Go back to the original research question and address it directly. If you rejected the null hypothesis, then there is convincing evidence that at least one of the population proportions is not as stated in the null hypothesis. If you failed to reject the null hypothesis, then there is not enough evidence that any of the population proportions are different from what is stated in the null hypothesis.
The Genius Blog
Hypothesis Testing Solved Examples(Questions and Solutions)
Here is a list hypothesis testing exercises and solutions. Try to solve a question by yourself first before you look at the solution.
Question 1 In the population, the average IQ is 100 with a standard deviation of 15. A team of scientists want to test a new medication to see if it has either a positive or negative effect on intelligence, or not effect at all. A sample of 30 participants who have taken the medication has a mean of 140. Did the medication affect intelligence? View Solution to Question 1
A professor wants to know if her introductory statistics class has a good grasp of basic math. Six students are chosen at random from the class and given a math proficiency test. The professor wants the class to be able to score above 70 on the test. The six students get the following scores:62, 92, 75, 68, 83, 95. Can the professor have 90% confidence that the mean score for the class on the test would be above 70. Solution to Question 2
Question 3 In a packaging plant, a machine packs cartons with jars. It is supposed that a new machine would pack faster on the average than the machine currently used. To test the hypothesis, the time it takes each machine to pack ten cartons are recorded. The result in seconds is as follows.
| 42.1 | 42.7 |
| 41 | 43.6 |
| 41.3 | 43.8 |
| 41.8 | 43.3 |
| 42.4 | 42.5 |
| 42.8 | 43.5 |
| 43.2 | 43.1 |
| 42.3 | 41.7 |
| 41.8 | 44 |
| 42.7 | 44.1 |
Do the data provide sufficient evidence to conclude that, on the average, the new machine packs faster? Perform the required hypothesis test at the 5% level of significance. Solution to Question 3
Question 4 We want to compare the heights in inches of two groups of individuals. Here are the measurements: X: 175, 168, 168, 190, 156, 181, 182, 175, 174, 179 Y: 120, 180, 125, 188, 130, 190, 110, 185, 112, 188 Solution to Question 4
Question 5 A clinic provides a program to help their clients lose weight and asks a consumer agency to investigate the effectiveness of the program. The agency takes a sample of 15 people, weighing each person in the sample before the program begins and 3 months later. The results a tabulated below
Determine is the program is effective. Solution to Question 5
Question 6 A sample of 20 students were selected and given a diagnostic module prior to studying for a test. And then they were given the test again after completing the module. . The result of the students scores in the test before and after the test is tabulated below.
We want to see if there is significant improvement in the student’s performance due to this teaching method Solution to Question 6
Question 7 A study was performed to test wether cars get better mileage on premium gas than on regular gas. Each of 10 cars was first filled with regular or premium gas, decided by a coin toss, and the mileage for the tank was recorded. The mileage was recorded again for the same cars using other kind of gasoline. Determine wether cars get significantly better mileage with premium gas.
Mileage with regular gas: 16,20,21,22,23,22,27,25,27,28 Mileage with premium gas: 19, 22,24,24,25,25,26,26,28,32 Solution to Question 7
Question 8 An automatic cutter machine must cut steel strips of 1200 mm length. From a preliminary data, we checked that the lengths of the pieces produced by the machine can be considered as normal random variables with a 3mm standard deviation. We want to make sure that the machine is set correctly. Therefore 16 pieces of the products are randomly selected and weight. The figures were in mm: 1193,1196,1198,1195,1198,1199,1204,1193,1203,1201,1196,1200,1191,1196,1198,1191 Examine wether there is any significant deviation from the required size Solution to Question 8
Question 9 Blood pressure reading of ten patients before and after medication for reducing the blood pressure are as follows
Patient: 1,2,3,4,5,6,7,8,9,10 Before treatment: 86,84,78,90,92,77,89,90,90,86 After treatment: 80,80,92,79,92,82,88,89,92,83
Test the null hypothesis of no effect agains the alternate hypothesis that medication is effective. Execute it with Wilcoxon test Solution to Question 9
Question on ANOVA Sussan Sound predicts that students will learn most effectively with a constant background sound, as opposed to an unpredictable sound or no sound at all. She randomly divides 24 students into three groups of 8 each. All students study a passage of text for 30 minutes. Those in group 1 study with background sound at a constant volume in the background. Those in group 2 study with nose that changes volume periodically. Those in group 3 study with no sound at all. After studying, all students take a 10 point multiple choice test over the material. Their scores are tabulated below.
Group1: Constant sound: 7,4,6,8,6,6,2,9 Group 2: Random sound: 5,5,3,4,4,7,2,2 Group 3: No sound at all: 2,4,7,1,2,1,5,5 Solution to Question 10
Question 11 Using the following three groups of data, perform a one-way analysis of variance using α = 0.05.
| 51 | 23 | 56 |
| 45 | 43 | 76 |
| 33 | 23 | 74 |
| 45 | 43 | 87 |
| 67 | 45 | 56 |
Solution to Question 11
Question 12 In a packaging plant, a machine packs cartons with jars. It is supposed that a new machine would pack faster on the average than the machine currently used. To test the hypothesis, the time it takes each machine to pack ten cartons are recorded. The result in seconds is as follows.
New Machine: 42,41,41.3,41.8,42.4,42.8,43.2,42.3,41.8,42.7 Old Machine: 42.7,43.6,43.8,43.3,42.5,43.5,43.1,41.7,44,44.1
Perform an F-test to determine if the null hypothesis should be accepted. Solution to Question 12
Question 13 A random sample 500 U.S adults are questioned about their political affiliation and opinion on a tax reform bill. We need to test if the political affiliation and their opinon on a tax reform bill are dependent, at 5% level of significance. The observed contingency table is given below.
| total | ||||
| 138 | 83 | 64 | 285 | |
| 64 | 67 | 84 | 215 | |
| total | 202 | 150 | 148 | 500 |
Solution to Question 13
Question 14 Can a dice be considered regular which is showing the following frequency distribution during 1000 throws?
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 182 | 154 | 162 | 175 | 151 | 176 |
Solution to Question 14
Solution to Question 15
Question 16 A newly developed muesli contains five types of seeds (A, B, C, D and E). The percentage of which is 35%, 25%, 20%, 10% and 10% according to the product information. In a randomly selected muesli, the following volume distribution was found.
| Component | A | B | C | D | E |
| Number of Pieces | 184 | 145 | 100 | 63 | 63 |
Lets us decide about the null hypothesis whether the composition of the sample corresponds to the distribution indicated on the packaging at alpha = 0.1 significance level. Solution to Question 16
Question 17 A research team investigated whether there was any significant correlation between the severity of a certain disease runoff and the age of the patients. During the study, data for n = 200 patients were collected and grouped according to the severity of the disease and the age of the patient. The table below shows the result
| 41 | 34 | 9 | ||
| 25 | 25 | 12 | ||
| 6 | 33 | 15 | ||
Let us decided about the correlation between the age of the patients and the severity of disease progression. Solution to Question 17
Question 18 A publisher is interested in determine which of three book cover is most attractive. He interviews 400 people in each of the three states (California, Illinois and New York), and asks each person which of the cover he or she prefers. The number of preference for each cover is as follows:
| 81 | 60 | 182 | 323 | |
| 78 | 93 | 95 | 266 | |
| 241 | 247 | 123 | 611 | |
| 400 | 400 | 400 | 1200 |
Do these data indicate that there are regional differences in people’s preferences concerning these covers? Use the 0.05 level of significance. Solution to Question 18
Question 19 Trees planted along the road were checked for which ones are healthy(H) or diseased (D) and the following arrangement of the trees were obtained:
H H H H D D D H H H H H H H D D H H D D D
Test at the = 0.05 significance wether this arrangement may be regarded as random
Solution to Question 19
Question 20 Suppose we flip a coin n = 15 times and come up with the following arrangements
H T T T H H T T T T H H T H H
(H = head, T = tail)
Test at the alpha = 0.05 significance level whether this arrangement may be regarded as random.
Solution to Question 20
kindsonthegenius
You might also like, excel sheets for statistics with formulas for free, hypothesis testing problems – question 5 ( a clinic provides a program to…, how to perform analysis of variance (anova) – step by step procedure.
I am really impressed with your writing abilities as well as with the structure to your weblog. Is this a paid subject matter or did you modify it yourself?
Either way stay up the excellent high quality writing, it’s uncommon to look a great blog like this one these days..
Below are given the gain in weights (in lbs.) of pigs fed on two diet A and B Dieta 25 32 30 34 24 14 32 24 30 31 35 25 – – DietB 44 34 22 10 47 31 40 30 32 35 18 21 35 29
How to Solve Hypothesis Testing Problems
One common type of problem you will find in Basic Statistics homework is the type of problem that involves using sample data to test a hypothesis .
A hypothesis is a statement about a population parameter. This is, it is a claim that we make about a certain population parameter, such as the population mean, or the population standard deviation.
For example, an engineer from a car manufacturer may claim that the population mean gas mileage of a new car model is 25 mpg. That would be an hypothesis. Or for example, a political polls researcher may claim that the voting share of certain candidate is 53%. That would be another hypothesis, about the true proportion of voters who support that certain candidate.
Consider the following example : A psychologist claims that the mean IQ scores of statistics instructors is greater than 100. She collects sample data from 15 statistics instructors and she finds that \(\bar{X}=118\) and s = 11. The sample data appear to come from a normally distributed population with unknown \(\mu\) and \(\sigma\).
Let us solve this problem:
Notice that we want to test the following null and alternative hypotheses
\[\begin{align}{{H}_{0}}:\mu {\le} {100}\, \\ {{H}_{A}}:\mu {>} {100} \\ \end{align}\]
Considering that the population standard deviation \(\sigma\) is not provided, we have to use a t-test with the following formula:
\[t =\frac{\bar{X}-\mu }{s / \sqrt{n}}\]
This corresponds to a right-tailed t-test. The t-statistics is given by the following formula:
\[t=\frac{\bar{X}-\mu }{s /\sqrt{n}}=\frac{{118}-100}{11/\sqrt{15}}={6.3376}\]
The critical value for \(\alpha = 0.05\) and for \(df = n- 1 = 15 -1 = 14\) degrees of freedom for this right-tailed test is \(t_{c} = 1.761\). The rejection region is given by
\[R = \left\{ t:\,\,\,t>{ 1.761 } \right\}\]
Since \(t = 6.3376 {>} t_c = 1.761\), then we reject the null hypothesis H 0 .
Alternatively, we can use the p-value approach. The right-tailed p-value for this test is calculated as
\[p=\Pr \left( {{t}_{14}}>6.3376 \right)=0.000\]
Considering that the p-value is such that \(p = 0.000 {<} 0.05\), we reject the null hypothesis H 0 .
Hence, we have enough evidence to support the claim that the mean IQ scores of statistics instructors is greater than 100.
log in to your account
Reset password.

IMAGES
VIDEO
COMMENTS
Fifteen randomly chosen teenagers were asked how many hours per week they spend on the phone. The sample mean was 4.75 hours with a sample standard deviation of 2.0. Conduct a hypothesis test. The null and alternative hypotheses are: H0: ˉx = 4.5, Ha: ˉx> 4.5 H 0: x ¯ = 4.5, H a: x ¯> 4.5.
raw cornstarch diet has a mean glucose level of 135 with a standard d. = 25 = 0.10Step 1: State the null and alternative hypothes. = 120 : ≠ 120Step 2: Determine the test statistic, then compute its value.= 24Since it is the population mean being tested, the population st. is unknown, a.
Table of contents. Step 1: State your null and alternate hypothesis. Step 2: Collect data. Step 3: Perform a statistical test. Step 4: Decide whether to reject or fail to reject your null hypothesis. Step 5: Present your findings. Other interesting articles. Frequently asked questions about hypothesis testing.
This statistics video tutorial explains how to solve hypothesis testing problems with proportions. It explains how to calculate the sample proportion and th...
Step 1: State the Null Hypothesis. The null hypothesis can be thought of as the opposite of the "guess" the researchers made: in this example, the biologist thinks the plant height will be different for the fertilizers. So the null would be that there will be no difference among the groups of plants. Specifically, in more statistical language ...
Hypothesis testing is based directly on sampling theory and the probabilities P(test statistic ∣ H0) P ( test statistic ∣ H 0) that the sampling theory gives. Here are the steps we will follow : Hypotheses : Formulate H0 H 0 and H1 H 1. State which is the claim. Critical statistic : Find the critical values and regions.
The mean length of time in jail from the survey was 3 years with a standard deviation of 1.8 years. Suppose that it is somehow known that the population standard deviation is 1.5. If you were conducting a hypothesis test to determine if the mean length of jail time has increased, what would the null and alternative hypotheses be?
If the biologist set her significance level \(\alpha\) at 0.05 and used the critical value approach to conduct her hypothesis test, she would reject the null hypothesis if her test statistic t* were less than -1.6939 (determined using statistical software or a t-table):s-3-3. Since the biologist's test statistic, t* = -4.60, is less than -1.6939, the biologist rejects the null hypothesis.
A hypothesis test is a statistical inference method used to test the significance of a proposed (hypothesized) relation between population statistics (parameters) and their corresponding sample estimators. In other words, hypothesis tests are used to determine if there is enough evidence in a sample to prove a hypothesis true for the entire population. The test considers two hypotheses: the ...
Step 1: State the Null Hypothesis. The null hypothesis can be thought of as the opposite of the "guess" the researchers made. In the example presented in the previous section, the biologist "guesses" plant height will be different for the various fertilizers. So the null hypothesis would be that there will be no difference among the groups of ...
9.1 Hypothesis Testing Problem Solving Steps Now that we have some background on setting up hypotheses and finding critical regions, we introduce the steps needed for every hypothesis testing procedure. Hypothesis testing is based directly on sampling theory and the probabilities that the sampling theory gives. Here are the steps we will follow :
Set up the Hypothesis Test: Since the problem is about a mean, this is a test of a single population mean. Set the null and alternative hypothesis: In this case there is an implied challenge or claim. This is that the goggles will reduce the swimming time. The effect of this is to set the hypothesis as a one-tailed test.
1. Defining Your Hypothesis. An hypothesis test is usually composed by. Null Hypothesis (H0, read "H zero"): states that all things remain equal. No phenomena is observed or there is not relationship between what you are comparing; Alternative Hypothesis (H1, read "H one"): states the opposite of the Null Hypothesis. That there was some ...
When using the p-value to evaluate a hypothesis test, the following rhymes can come in handy:. If the p-value is low, the null must go.. If the p-value is high, the null must fly.. This memory aid relates a p-value less than the established alpha ("the p-value is low") as rejecting the null hypothesis and, likewise, relates a p-value higher than the established alpha ("the p-value is ...
The data are assumed to be from a normal distribution. Answer. Set up the hypothesis test: A 5% level of significance means that α = 0.05 α = 0.05. This is a test of a single population mean. H0: μ = 65 Ha: μ> 65 H 0: μ = 65 H a: μ> 65. Since the instructor thinks the average score is higher, use a ">> ".
The null hypothesis has the same parameter and number with an equal sign. H0: μ = $30, 000 HA: μ> $30, 000. b. x = number od students who like math. p = proportion of students who like math. The guess is that p < 0.10 and that is the alternative hypothesis. H0: p = 0.10 HA: p <0.10. c. x = age of students in this class.
Step 1: Check assumptions and write hypotheses. When conducting a chi-square goodness-of-fit test, it makes the most sense to write the hypotheses first. The hypotheses will depend on the research question. The null hypothesis will always contain the equalities and the alternative hypothesis will be that at least one population proportion is ...
View Solution to Question 1. Question 2. A professor wants to know if her introductory statistics class has a good grasp of basic math. Six students are chosen at random from the class and given a math proficiency test. The professor wants the class to be able to score above 70 on the test. The six students get the following scores:62, 92, 75 ...
1. identify the steps in hypothesis testing; and. 2. solve problems involving test of hypothesis on the population mean. Before you proceed to the lesson, make sure to answer first the questions on the "What I Know" portion. Statistics and Probability Quarter 4 Self-Learning Module: Solving Problems Involving Test of Hypothesis on ...
From the t-value table at. .10 level of significance, the critical value is ±1.711.Step 4: Draw a conclusion.Since the t-computed value is 1.974 which is greater than the critical. alue of 1.711, we reject the null hypothesis and support the alternative hypothesis. We can conclude that there is enough evidenc.
SP-LAS-8-Quarter-4-MELC-8 - Free download as PDF File (.pdf), Text File (.txt) or read online for free.
Example 8.4.7. Joon believes that 50% of first-time brides in the United States are younger than their grooms. She performs a hypothesis test to determine if the percentage is the same or different from 50%. Joon samples 100 first-time brides and 53 reply that they are younger than their grooms.
Although problem solving has steps, someone may have his/her own way or techniques of solving a problem. Meanwhile, in statistical analysis, there are steps that need to be followed in solving problems involving test of hypothesis on population proportion. The objective is for us to make a correct decision about the null hypothesis.
How to Solve Hypothesis Testing Problems One common type of problem you will find in Basic Statistics homework is the type of problem that involves using sample data to test a hypothesis . A hypothesis is a statement about a population parameter. This is, it is a claim that we make about a certain population parameter, such as the population ...
This framework over proper hypothesis testing is the basis of the Bayesian vs Frequentist controversy. Consider the independent sample t-test (see Chapter 8.5 and 8.6 ... Turns out there is a lot of philosophical problems around the idea of "probability," and three schools of thought. In the Fisherian approach to testing, the researcher ...